Nos exercícios de a esboce o gráfico da função.
4)
Passo 1
Cara, nesse problema, poderíamos resolvê-lo de duas maneiras:
1º - Fazendo um monte de passo a passo encontrando domínio, intervalos de crescimento, etc.
2º - Fazer utilizando transformações de gráficos que já conhecemos.
A primeira maneira de se resolver é interessante quando temos uma função absurdamente complicada e que não temos uma noção muito clara de quem ela poderia ser. Mas, em casos que conseguimos dizer por alto qual é a cara da função, o segundo método é mais rápido.
Como conhecemos bem a cara da função ...
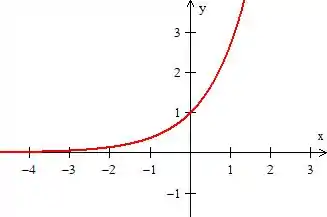
Podemos trabalhar um pouco com ela para chegar na que queremos...
Bora? :D
Passo 2
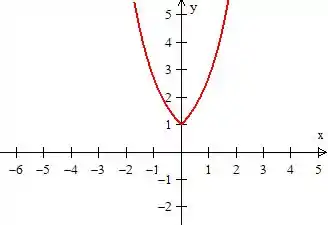
Pow, se a função tivesse um módulo ao redor de , isso significaria que ao redor do eixo (onde , troca de sinal), teríamos uma reflexão do gráfico da função a direita (como uma simetria). Logo, se o gráfico de é
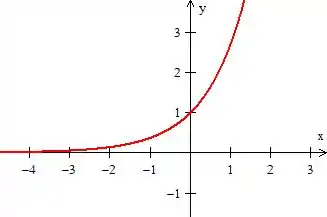
O gráfico de será...
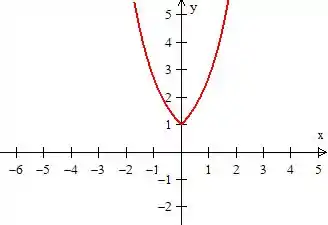
Repare que aquela “rabeta” da função exponencial desparece e dá lugar a parte simétrica da parte positiva. Isso acontece porque o módulo troca o sinal de , então mesmo quando é negativo, a exponencial terá o mesma aparência de como se ela fosse positiva, saca?
Passo 3
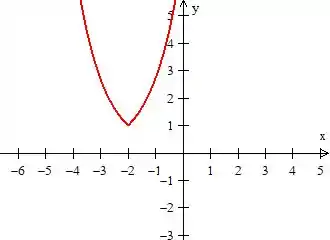
Toda vez que adicionamos um número dentro da função junto com o argumento , o que estamos fazendo é deslocando a função inteira a esquerda em cima do número (como se o eixo mudasse para aquele ponto).
Então se é assim...
O será...
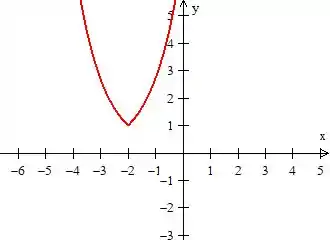
Tome muito cuidado, pois é sempre uma translação contrária ao senso comum: ora, como adicionamos ao , poderíamos pensar em puxar a função para cima do , mas não é assim, e sim o contrário, ok?
Passo 4
E prontinho! Já chegamos ao gráfico pedido de forma muito mais rápido, sacou?
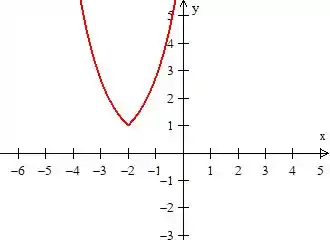
Resposta