Um atleta consegue correr em relação ao solo com velocidade e nadar com velocidade em relação à água. Ele quer atravessar um rio de corrente homogênea, cuja correnteza possui velocidade em relação às margens , saindo do ponto A e chegando ao ponto C, diretamente do outro lado da margem, como na figura. Como a temperatura da água está muito baixa, ele quer atravessar o rio, as águas o deslocam de seu objetivo, fazendo-o chegar do outro lado no ponto B. Considere as velocidades constantes e que .
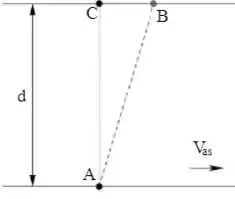
2) assim que chega em B, o atleta corre pelo solo, com a velocidade , para ir até C. Qual é o tempo total gasto pelo atleta desde o instante que saiu de A até chegar em C, seu objetivo?
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema é o seguinte: um atleta foi atravessar o rio nadando, mas a correnteza acabou levando-o para o ponto B, ao invés de ir direto para o ponto C.
No primeiro item calculamos a distância entre os pontos BC, e esse resultado vai ser muito útil aqui:
Agora o problema pede para calcularmos o tempo gasto para percorrer essa distância

Mas como temos a distância e sabemos que a velocidade que ele anda no chão é constante, é só jogar tudo na equação do MRU

E é isso que vamos fazer! Bora lá?
Passo 2
A velocidade que o homem anda no chão é e a distância percorrida foi de , agora é só substituir:
E é isso!
Espero ter ajudado!