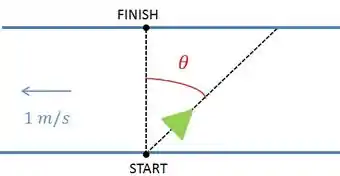
Uma garota deseja cruzar um rio nadando diretamente ao ponto oposto na outra margem, como mostrado na figura. Ela pode nadar a uma velocidade de em relação à água e o rio está fluindo a. Em que ângulo em relação à linha que une o ponto de largada (Start) e o ponto de chegada (Finish) ela deve nadar?

a.

b.

c.

d.

e.

Ele fala pra gente o seguinte:

A velocidade da garota em relação à agua é .

A velocidade da água em relação à margem é .

Vamos desenhar o que ele tá falando pra gente.

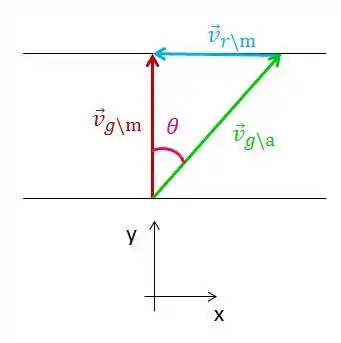
Então, daí a gente pode tirar duas relações:

Uma pela soma vetorial:

E a outra em relação ao módulo dos vetores, usando pitágoras:

Vamos usar essa segunda:

Beleza, já sabemos o módulo do vetor. Agora vamos usar aquela primeira equação para descobrirmos o ângulo.

Decompondo o vetor em suas componentes:

Igualando componente a componente:

E

Logo

Show!!!