A neve cai, verticalmente, com uma velocidade constante de . O motorista de um carro, viajando em linha reta numa estrada com uma velocidade de , vê os flocos de neve caírem formando um ângulo com a vertical. O valor deste ângulo é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos começar desenhando o que o enunciado está dizendo.
Primeiro, sabemos que a neve está caindo com uma velocidade que aponta verticalmente para baixo:
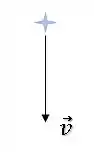
Enquanto isso, temos um carro andando numa linha reta com velocidade :
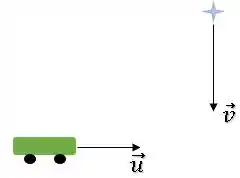
Mas uma velocidade depende de um referencial, certo?
Essas velocidades do desenho, por exemplo, estão em relação a um observador externo, ou seja estão sendo vistas por alguém em repouso do lado de fora.
Mas para resolver a questão, precisamos da velocidade da neve sendo vista pelo motorista do carro, ou seja, a velocidade da neve com relação ao carro .
Para isso, basta subtrair a velocidade do carro da velocidade da neve , isso porque ambas estão com relação ao mesmo observador externo:
Lembrando que para subtrair vetores, basta somar com o vetor na direção oposta:
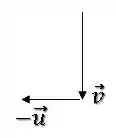
Então, o nosso vetor resultante será:
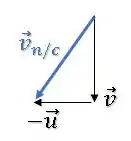
Passo 2
Agora que já sabemos quem é o vetor da velocidade da neve com relação ao carro , queremos o valor do ângulo que ele faz com a vertical.
Vamos chamar esse ângulo de .
Então, estará aqui:
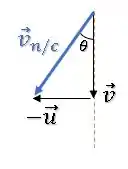
Como o vetor ou está na horizontal, enquanto o vetor está na vertical, eles fazem entre si.
Então, podemos simplesmente usar as relações de um triângulo retângulo para achar .
Lembrando que o comprimento dos catetos do triângulo vão ser os módulos dos vetores, ou seja e :
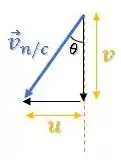
Para relacionar os dois catetos, vamos usar a tangente:
Como queremos o ângulo em si, vamos isolar usando a função inversa da tangente dos dois lados:
Achamos a resposta da letra (b).
Resposta
Letra (b)