Movimento Relativo e Referencial
Um observador parado no solo vê um pacote caindo de um avião, com velocidade de módulo igual a , mas que faz um certo ângulo com a vertical; considere a Terra um referencial inercial. Simultaneamente o piloto do avião, que voa na horizontal com velocidade constante, vê o mesmo pacote caindo na vertical, com velocidade de módulo igual a . O módulo da velocidade do avião em relação ao observador no solo é
Passo 1
Pelo enunciado temos que a velocidade do pacote é inclinada, para direita e para baixo, enquanto a velocidade relativa do pacote para o avião é para baixo.
Vamos fazer um esquema disso
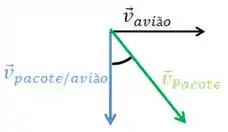
A fórmula de velocidade relativa nos diz que
Podemos reescrever
Ou seja, a e são componentes da velocidade do pacote.
Passo 2
O módulo da velocidade do pacote é
Resposta
Letra A
Exercícios de Livros Relacionados
Um avião pequeno atinge uma velocidade do ar de 500k m / h . O piloto pretende chegar a um ponto 800k m ao norte, mas descobre que deve direcionar o avião 20,0 ° a leste do norte para atingir o destin
A ‘esteira rolante horizontal’ do terminal de um aeroporto se move a 1,0m/s e tem 35,0m de comprimento. Se uma mulher pisa em uma das extremidades e caminha a 1,5m/s em relação à plataforma móvel, qua
Dois píeres estão localizados em um rio: o píer B está situado a 1500 m de A corrente abaixo (Figura 3.35). Dois amigos devem fazer um percurso do píer A ao píer B e depois voltar. Umdeles vai de barc
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Um rio de 1km de largura tem uma correnteza de velocidade 1,5 km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 km/h em relação à água. a) Qual é o tempo mínimo que leva para at