Vista de um referencial fixo nas escretas e centrado no Sol, a Terra tem vetor velocidade dado em um certo instante por e um foguete em translação tem velocidade constante , como mostra a figura. Considerando o foguete como um referencial com eixos coordenados , , e de mesmas direções e sentidos que os respectivos eixos , e , o vetor velocidade da Terra relativo a ele é
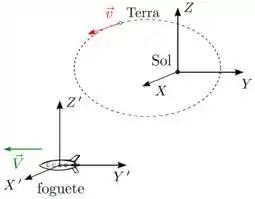
Passo 1
Nesse caso temos uma situação levemente diferente do que estamos acostumados, mas fique tranqüilo que é quase igual.
Como a terra está se mexendo, e o foguete também, iremos considerar o referencial deles dois como sendo o Sol. Essa é a única mudança. Os dados do problema são
Pela fórmula de velocidade relativa
Resposta
Letra
Exercícios de Livros Relacionados
Um avião pequeno atinge uma velocidade do ar de 500k m / h . O piloto pretende chegar a um ponto 800k m ao norte, mas descobre que deve direcionar o avião 20,0 ° a leste do norte para atingir o destin
A ‘esteira rolante horizontal’ do terminal de um aeroporto se move a 1,0m/s e tem 35,0m de comprimento. Se uma mulher pisa em uma das extremidades e caminha a 1,5m/s em relação à plataforma móvel, qua
Dois píeres estão localizados em um rio: o píer B está situado a 1500 m de A corrente abaixo (Figura 3.35). Dois amigos devem fazer um percurso do píer A ao píer B e depois voltar. Umdeles vai de barc
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Um rio de 1km de largura tem uma correnteza de velocidade 1,5 km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 km/h em relação à água. a) Qual é o tempo mínimo que leva para at