Movimento Relativo e Referencial
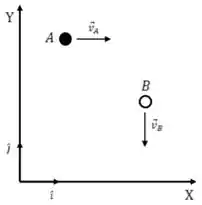
Duas partículas e movem-se no plano horizontal , respectivamente com velocidades e constantes. A direção do movimento de é perpendicular ao eixo e a direção do movimento de é perpendicular ao eixo ; vide a figura abaixo. Seja a velocidade de com relação a a opção correta é:
- , pois é perpendicular a
- Todas as opções acima estão erradas
Passo 1
Temos os seguintes dados do enunciado
Pela fórmula de velocidade relativa temos que
Passo 2
Vamos agora achar o módulo de
Resposta
Letra B
Exercícios de Livros Relacionados
Um avião pequeno atinge uma velocidade do ar de 500k m / h . O piloto pretende chegar a um ponto 800k m ao norte, mas descobre que deve direcionar o avião 20,0 ° a leste do norte para atingir o destin
A ‘esteira rolante horizontal’ do terminal de um aeroporto se move a 1,0m/s e tem 35,0m de comprimento. Se uma mulher pisa em uma das extremidades e caminha a 1,5m/s em relação à plataforma móvel, qua
Dois píeres estão localizados em um rio: o píer B está situado a 1500 m de A corrente abaixo (Figura 3.35). Dois amigos devem fazer um percurso do píer A ao píer B e depois voltar. Umdeles vai de barc
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Um rio de 1km de largura tem uma correnteza de velocidade 1,5 km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 km/h em relação à água. a) Qual é o tempo mínimo que leva para at