Um barco encontra-se em repouso em relação à água de um rio. A correnteza do rio tem velocidade de em relação às margens, se movendo em direção ao norte. Uma pessoa anda dentro do barco para o leste, com velocidade de . Qual é a direção do movimento da pessoa em relação às margens? E qual o módulo de sua velocidade?
- Para o leste,
- Para o sudeste,
- Para o norte,
- Para o nordeste,
- Para o sudeste,
Passo 1
Pensa bem, se o barco está em repouso em relação ao rio, nosso referencial tem uma complicação a menos! Então podemos empurrar na água nosso colega e fazer as contas com ele lá. Representando a velocidade do rio e do barco/pessoa empurrada como vetores, vamos ter:
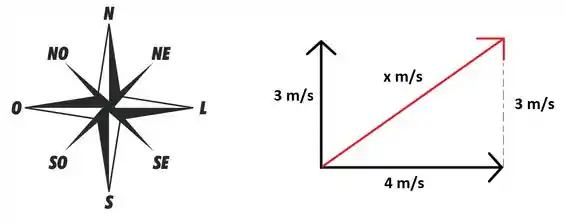
O vetor resultante é o em vermelho e veja só! Ele aponta pro nordeste! Agora que sabemos direção e sentido, pelo teorema de Pitágoras:
Resposta
Exercícios de Livros Relacionados
Um avião pequeno atinge uma velocidade do ar de 500k m / h . O piloto pretende chegar a um ponto 800k m ao norte, mas descobre que deve direcionar o avião 20,0 ° a leste do norte para atingir o destin
A ‘esteira rolante horizontal’ do terminal de um aeroporto se move a 1,0m/s e tem 35,0m de comprimento. Se uma mulher pisa em uma das extremidades e caminha a 1,5m/s em relação à plataforma móvel, qua
Dois píeres estão localizados em um rio: o píer B está situado a 1500 m de A corrente abaixo (Figura 3.35). Dois amigos devem fazer um percurso do píer A ao píer B e depois voltar. Umdeles vai de barc
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Um rio de 1km de largura tem uma correnteza de velocidade 1,5 km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 km/h em relação à água. a) Qual é o tempo mínimo que leva para at