Um rio de 200 m de largura corre com uma velocidade uniforme de através de uma floresta, na direção oeste. Um explorador deseja sair de uma pequena clareira na margem sul e atravessar o rio em um barco a motor que se move com uma velocidade escalar constante de em relação à água. Existe uma outra clareira na margem norte, rio acima a partir de um ponto da margem sul, exatamente em frente à clareira. Em que direção o barco deve ser apontado para viajar em linha reta e chegar à clareira da margem norte? Quanto tempo o barco leva para atravessar o rio e chegar à clareira?
Passo 1
Primeiro vamos desenhar o que o problema que temos, para entendermos mlhor o que está acontecendo. Esse seria um esboço com o sdados que ele no deu.
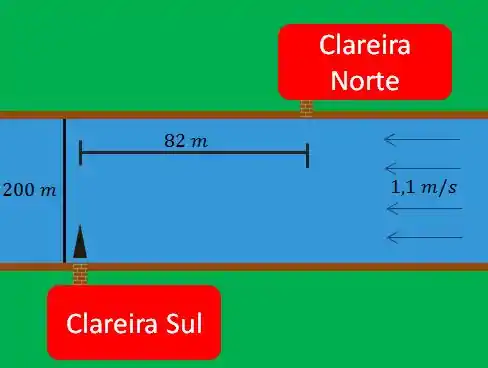
Vamos resolver essa questão usando o vetor posição relativa. Cosiderando que o barquinho está na origem do nosso eixo no porto sul.
Vamos enterder primeiro o que faremos. A linha tracejada significa a linha reta que o barquinho deve andar para chegar do porto sul até o porto norte.
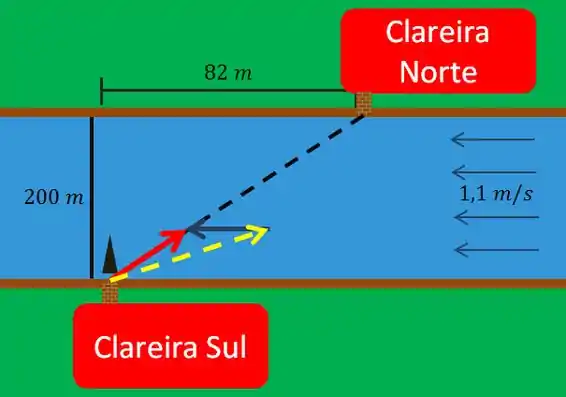
A seta azul escuro simboliza o deslocamento da água em relação ao porto sul. A seta vermelha o deslocamento do barco em relação ao porto sul e a seta amarela o deslocamento do barco em relação a água , ou seja, a pra onde o barco deve ser apontado.
Passo 2
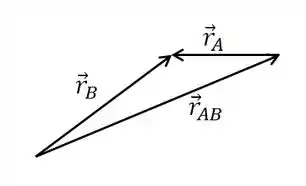
Temos então e quer chegar na posição . Ambas posições são em relação a origem no porto sul (referêncial parado). Logo o deslocamento do barquinho seria
Passo 3
Sabemos que a água desloca-se com velocida , pela equação da posição descobrimos
Passo 4
Vamos então calcular o vetor posição relativa do barco em relação a água pela equação
Terminamos de descobrir a equação para o vetor posição do barco em relação a água, porém ela está em função do tempo e por isso vamos primeiro descobrir o valor de .
Passo 5
Como o problema também nos fornecer o módulo da velocidade do barco em relação a água .
Pela equação da posição de um movimento uniforme temos:
Como temos o módulo do vetor velocidade e pelo tempo ser sempre positivo podemos dizer que
Tirando a raíz
Passo 6
Substituindo na equação do vetor posição temos:
Com esse vetor já temos representado a direção em que o barco deve ser apontado, porém se quisermos completar a resposta podemos dar o ângulo que o barco deve ser apontado em relação a margem sul do rio.
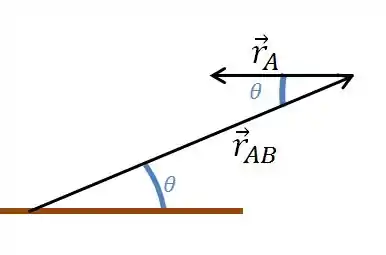
Como é horizontal (mesma direção da margem), temos que o ângulo entre os dois vetores é igual ao ângulo de com a margem sul.
Já vimos uma fórmula para calcular ângulo entre vetores, que é