Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Relativo Bidimensional

Ver Teoria
Exercício 56123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555758

Enunciado

Movimento Relativo e Referencial

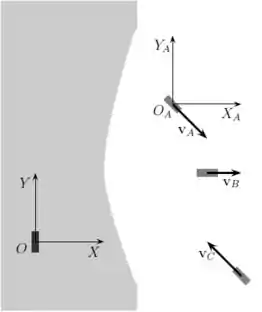
Em um lago tranqüilo três barcos A , B e C têm velocidades respectivas v → A = v i ^ - v j ^ , v → B = v i ^ e v → C = - v i ^ + v j ^ ( v uma constante dada), todas relativas ao referencial constituído por um ônibus estacionado na margem com um sistema de eixos O X Y Z , sendo O X Y na horizontal, conforme a figura. Considere o barco A como um referencial com sistema de eixos O A X A Y A Z A , cada um deles com mesma direção e sentido dos respectivos eixos de O X Y Z . Em relação ao referencial do barco A as velocidades do ônibus, do barco B e do barco C são, respectivamente,

  1. v → ' O   = - v i ^ + v j ^ , v → ' B = v j ^ e v → ' C = - 2 v i ^ + 2 v j ^
  2. v → ' O   = v i ^ + v j ^ , v → ' B = v j ^ e v → ' C = 2 v i ^ + 2 v j ^
  3. v → ' O   = - v i ^ + v j ^ , v → ' B = v j ^ e v → ' C = - 2 v i ^ - 2 v j ^
  4. v → ' O   = v i ^ - v j ^ , v → ' B = v j ^ e v → ' C = 2 v i ^ + 2 v j ^
  5. Nenhuma das respostas anteriores

Passo 1

Os dados do enunciado são

Dados v → O = 0 → v → A = v i ^ - v j ^ v → B = v i ^ v → C = - v i ^ + v j ^

O que significa achar a velocidade no referencial do barco A ? Ele quer a velocidade de cada um relativa ao barco A . Vamos escrever a fórmula genericamente

v → i / A = v → i - v → A

Onde i é um dos barcos ou o ônibus.

Passo 2

Vamos começar achando a velocidade relativa do ônibus.

v → O ' = v → O - v → A

v → O ' = 0 - v i ^ - v j ^

v → O ' = - v i ^ + v j ^

Passo 3

A velocidade do barco B em relação ao barco A é dada por:

v → B ' = v → B - v → A

v → B ' = v i ^ - v i ^ - v j ^

v → B ' = v i ^ - v i ^ + v j ^

v → B ' = v j ^

Passo 4

A velocidade do barco C em relação ao barco A é dada por:

v → C ' = v → C - v → A

v → C ' = - v i ^ + v j ^ - v i ^ - v j ^

v → C ' = - v i ^ + v j ^ - v i ^ + v j ^

v → C ' = - 2 v i ^ + 2 v j ^

Passo 5

Recapitulando, temos

v → O ' = - v i ^ + v j ^

v → B ' = v j ^

v → C ' = - 2 v i ^ + 2 v j ^

Resposta

Letra A

Exercícios de Livros Relacionados

Um avião pequeno atinge uma velocidade do ar de 500k m / h . O piloto pretende chegar a um ponto 800k m ao norte, mas descobre que deve direcionar o avião 20,0 ° a leste do norte para atingir o destin
A ‘esteira rolante horizontal’ do terminal de um aeroporto se move a 1,0m/s e tem 35,0m de comprimento. Se uma mulher pisa em uma das extremidades e caminha a 1,5m/s em relação à plataforma móvel, qua
Dois píeres estão localizados em um rio: o píer B está situado a 1500 m de A corrente abaixo (Figura 3.35). Dois amigos devem fazer um percurso do píer A ao píer B e depois voltar. Umdeles vai de barc
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Um rio de 1km de largura tem uma correnteza de velocidade 1,5 km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 km/h em relação à água. a) Qual é o tempo mínimo que leva para at