Parte II - Duas rodovias se cruzam conforme a figura.
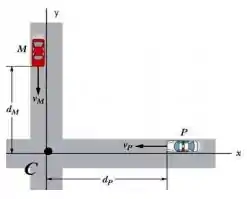
Um carro de polícia P se dirige para o cruzamento, estando distante do ponto C, com o mostrador do velocímetro indicando . Um outro carro M se move pela outra rodovia na direção do ponto de cruzamento, encontrando-se a uma distância , com velocidade escalar .
- Obtenha a velocidade do carro de polícia em relação ao carro M usando a notação de vetores unitários cartesianos.
- No instante mostrado na figura, determine o ângulo entre a reta que liga os dois carros e a velocidade relativa obtida no item (a) anterior.
Passo 1
Parte II - A seguir, estão representados o par de eixos escolhidos para a resolução da questão, assim como o vetores unitários e .
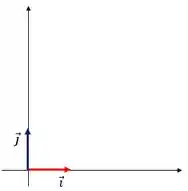
a) Calcularemos a velocidade do carro de polícia em relação ao carro M.
Colocando as velocidades na notação dos vetores unitários, teremos:
Lembrando que a velocidade de P em relação a M é calculada como:
Temos que:
Passo 2
b) Calculando o ângulo entre a reta que liga os dois carros e a velocidade relativa obtida em (a):
Sabendo que a posição dos carros na notação dos vetores unitários é dada por:
e
E que a posição relativa é calculada de acordo com a seguinte relação:
Temos:
Utilizando a fórmula do produto escalar para o cálculo do ângulo () entre os vetores de posição relativa e velocidade relativa: