Um navio está ao norte e a leste do navio . O navio está navegando com uma velocidade constante de na direção sul; o navio navega com uma velocidade constante de em direção ao norte do leste.
Escreva uma expressão para o vetor posição de em relação à em função do tempo considerando o instante como o instante e que os navios estão nas posições iniciais descritas acima. (Sugestão: faça um desenho para orientá-lo na sua solução posicionando o navio na origem do sistema de coordenadas em ).
Dados:
Passo 1
Antes de começar a calcular o vetor posição, vamos primeiro fazer um desenho esquemático. Desenhar é a melhor forma de não se confundir e de visualizar tudo que está acontecendo.
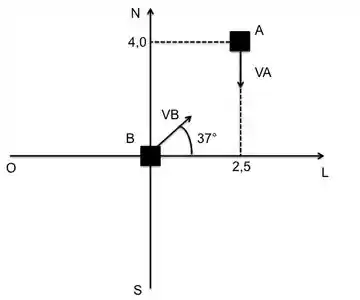
Agora podemos calcular o vetor posição!
Passo 2
Para calcular o vetor posição do navio em relação ao navio , devemos relembrar da fórmula de movimento relativo, temos que:
Onde e o vetor posição do navio em relação ao navio . e são os vetores posição dos navios e respectivamente.
Para determinar , devemos primeiro achar o vetor posição de cada navio em relação ao mar.
Passo 3
Vamos primeiro calcular o vetor posição do navio . Para facilitar, iremos trabalhar com as componentes e . Então, vamos lá!
Como o navio não possui movimento horizontal, temos que a componente do vetor posição é:
Em , temos uma velocidade que aponta no sentido negativo, dessa maneira, nosso vetor posição será:
Ou seja, o vetor posição do navio será:
Passo 4
Vamos agora calcular o vetor posição do navio . Para determinar o vetor posição de cada componente, devemos decompor a velocidade.
Em :
Como o navio se encontra na origem, o vetor posição será dado apenas pela componente da velocidade vezes o tempo.
Em :
Ou seja, o vetor posição do navio será:
Passo 5
Agora que temos o vetor posição de ambos os navios, podemos calcular .