Um atleta consegue correr em relação ao solo com velocidade e nadar com velocidade em relação à água. Ele quer atravessar um rio de corrente homogênea, cuja correnteza possui velocidade em relação às margens , saindo do ponto A e chegando ao ponto C, diretamente do outro lado da margem, como na figura. Como a temperatura da água está muito baixa, ele quer atravessar o rio, as águas o deslocam de seu objetivo, fazendo-o chegar do outro lado no ponto B. Considere as velocidades constantes e que .
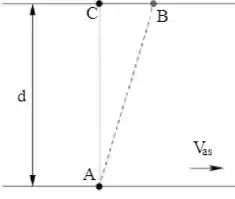
3) qual foi a velocidade vetorial média do atleta no percurso (módulo, direção e sentido)? Considerando a distância total percorrida, qual foi sua velocidade escalar média?
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema é o seguinte: um atleta foi atravessar o rio nadando, mas a correnteza acabou levando-o para o ponto B, ao invés de ir direto para o ponto C.
No primeiro item calculamos a distância entre os pontos BC, e esse resultado vai ser muito útil aqui:
Também calculamos o tempo que ele levou para ir de A até B:
Agora o problema nos pede para calcular a velocidade vetorial média do atleta e depois a velocidade escalar média

A velocidade vetorial é dada pela variação vetorial da posição pela variação total do tempo . A variação do tempo é a soma dos tempos nos dois trechos: . Já temos , falta determinar .
E a variação da posição? Bom, para vermos melhor, dá uma olhadinha nesse desenho aqui:
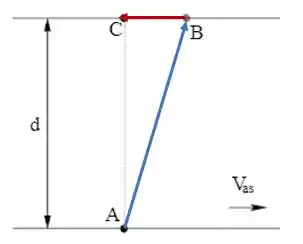
Em um primeiro momento o atleta percorreu o trajeto em azul AB, dentro da água. Depois (em vermelho) correu pela margem de B para C, seu ponto final. A soma vetorial pode ser feita unindo o início do primeiro vetor (azul) com a ponta da seta do segundo (vetor vermelho), resultando nesse vetor aqui em amarelo:
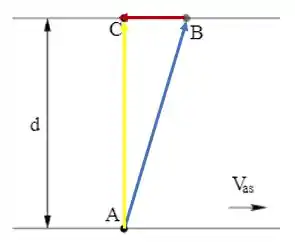
E esse vetor justamente é o vetor de módulo , vertical para cima! Assim é:

Beleza? Agora nosso próximo passo é determinar o tempo total, e por fim achar a velocidade vetorial média!
A velocidade escalar média envolve a distância total () pelo tempo total (adoro quando se recicla resultado kkk). Então depois de calcular a velocidade vetorial média, vamos calcular a velocidade escalar média.
Bora lá?
Passo 2
O tempo total é a soma dos temos nos trechos AB e BC. No treco AB o tempo gasto foi
Precisamos achar o tempo . Como a velocidade é constante, esse tempo será
Lembrando que o atleta nesse trecho corre no solo e tem velocidade .

O valor da distância entre B e C foi calculada no item 2 desse problema e vale:
Assim o tempo gasto nesse trecho é:
Certo?
E o tempo total é a soma :
Tranquilo até aqui?
Passo 3
Com o valor do vetor deslocamento e o tempo total, agora podemos calcular o vetor velocidade média:
Do passo 1:
Do passo 2:
Agora é só substituir:
Certo?
E a velocidade escalar média?
Passo 4
Como comentei lá no passo 1, a velocidade escalar média é a razão entre a distância total percorrida pelo tempo total transcorrido:
Então vai ser a soma dos deslocamentos em cima, e a soma dos tempos embaixo. A soma dos tempos nós já temos, e a distância também (). Só nos resta determinar . E aqui entra nosso bom e velho Pitágoras:
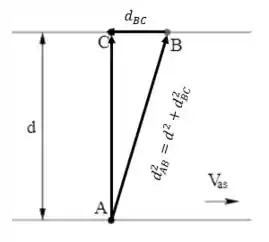
Assim a distância é:
E a distância total:
Tudo ok até aqui?

Com o tempo total e a distância total, podemos (até que enfim) calcular a velocidade escalar média:
A distância total:
Do passo 3 temos o tempo total:
A velocidade escalar:
Podemos ainda simplificar em todos os termos (até dentro da raiz, pois temos nos dois termos ali dentro) e só:
O restante fica assim mesmo, não temos uma graaande simplificação.
E é isso!
Espero ter ajudado!