Um homem a bordo de um bote a remo quer atravessar o canal entre São Sebastião e Ilha Bela no litoral norte de São Paulo de modo que a menor distância, que é de 3,0 km, seja percorrida. O homem consegue imprimir uma velocidade de módulo 2,0 m/s em relação à água. Considerando que no dia da travessia a correnteza no canal tem velocidade de 1,0m/s na direção perpendicular à direção da menor distância, a travessia demora:
Passo 1
Bom galera, um desenho esquemático que vai nos ajudar é esse aqui:
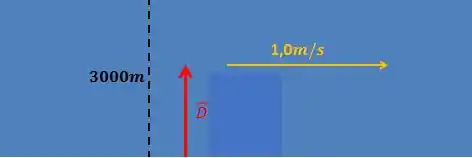
O vetor indica a direção de menor distância (vertical). Logo, a velocidade da correnteza tem o sentido da figura (horizontal).
Como o homem pretende ajustar a direção de sua velocidade de modo a atravessar a menor distância, a trajetória resultante do barco deve ser na direção de .
Mas como fazer o bote percorrer uma trajetória ao longo de se existe uma correnteza lateral de ?
Ele deve direcionar o bote de forma que a componente horizontal de sua velocidade com relação a água se cancele com a velocidade da correnteza.
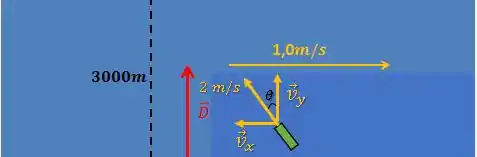
Dessa forma, para um observador fixo na margem, o bote estará cruzando o canal com uma velocidade na vertical apenas.
Passo 2
Vamos decompor a velocidade em suas componentes.
Na horizontal, temos:
Enquanto na vertical, temos:
Passo 3
Para que a velocidade resultante do barco na horizontal seja nula, temos que:
Assim, podemos encontrar o ângulo de inclinação da direção do bote:
Passo 4
Agora que já sabemos o ângulo da direção do bote com relação ao vetor , podemos encontrar o valor da componente vertical :
Passo 5
Agora que já sabemos a velocidade na direção de e a distância percorrida, podemos achar o tempo que leva a travessia:
Substitundo os valores, temos:
Podemos melhorar a cara dessa resposta racionalizando e colocando em notação científica:
Assim, ficamos com a letra (c).
Resposta
Letra (c)