Movimento Relativo e Referencial
O seguinte enunciado refere-se às questões e :
Um avião consegue viajar a uma velocidade de módulo em relação ao ar que o circunda. Tal avião quer seguir para o norte, enfrentando um vento de velocidade , onde a direção aponta para o leste e a direção aponta para o norte e é uma constante.
7. Para qual direção o avião deve apontar?
a) diretamente para o norte.
b) Para o nordeste, formando um ângulo de 26° em relação ao norte.
c) Para o nordeste, formando um ângulo de 30° em relação ao norte.
d) Para o noroeste, formando um ângulo de 30° em relação ao norte.
e) Para o noroeste, formando um ângulo de 26° em relação ao norte.
8. Qual é a velocidade de cruzeiro do avião (em relação ao chão).
a)
b)
c)
d)
e) nenhuma das anteriores.
Passo 1
7)
Vamos tentar representar esses vetores num eixo de coordenadas. O módulo do vetor velocidade do avião é e ele deseja caminhão para o norte, ou seja, na direção no sentido positivo. Para isso, ele precisa eliminar as componentes do vento, de forma que a componente do avião anulará a componente do vento, logo elas terão módulos iguais, mas sentidos diferentes. Vamos ver como fica.
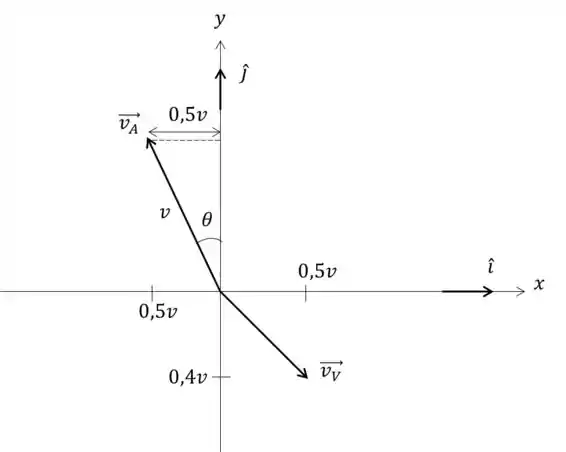
Conseguimos formar um triangulo retângulo para descobrir , temos que:
Portando o avião viajará para o noroeste fazendo um ângulo de 30°.
Passo 2
8)
Para achar a velocidade em relação ao solo, basta somar as componentes do vetor velocidade do avião com o vetor velocidade do vento, entretanto falta descobrir a componente do vetor velocidade do avião. Vamos aplicar Pitágoras:
Temos então:
Agora basta somar os vetores para achar o vetor resultante que é a velocidade do avião em relação ao solo.
Alternativa
Resposta
7) Alternativa
8) Alternativa