Parte I. Um estudante de física está dentro de um carro que segue a uma velocidade constante de na direção norte sob uma forte chuva que bate no carro da direção noroeste ( a oeste do norte) com velocidade constante de . Assinale as afirmativas verdadeiras sobre a velocidade do estudante em relação à chuva:
(a) seu módulo é igual a .
(b) sua direção é para a norte do leste.
(c) seu módulo é igual a .
(d) sua direção é para a sul do oeste.
(e) nenhuma das respostas é verdadeira.
Parte II. Suponha agora que dois pássaros, buscando abrigo contra a chuva, são vistos pelo estudante no carro: um pássaro () voando com velocidade constante de na direção sudeste ( ao sul do leste) e outro pássaro () voando acelerado em uma direção desconhecida. O estudante determina a equação da trajetória do pássaro dada por: . Determine , a velocidade do pássaro em relação ao pássaro .
Passo 1
Parte I. Podemos obter a velocidade resultante realizando a soma vetorial da velocidade do carro( com a velocidade do vento()
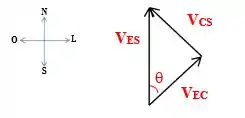
Substituindo os valores:
Portanto, o ângulo entre as componentes horizontal e vertical é dado por:
Além disso, o módulo é dado por
O que nos dá como resposta a letra (e)
Passo 2
Parte II.
Para encontrar a velocidade, usaremos a equação da velocidade relativa:
Onde é a velocidade do pássaro B em relação ao estudante, é a velocidade do pássaro B em relação ao pássaro A, o que estamos buscando e finalmente é a velocidade do pássaro A em relação ao estudante.
Calculando , temos:
O enunciado nos diz que é de a sudeste, então:
E então, usando a primeira equação:
Resposta
Parte I: (e)
Parte II: