[UFABC] Cálculo 1 – Lista 5 – Funções de Uma Variável – Questão 3
Uma calha deve ser construída com uma folha de metal de largura , dobrando-se para cima da folha de cada lado, fazendo-se um ângulo com a horizontal. Como deve ser escolhido de forma que a capacidade de carregar a água na calha seja máxima?
Passo 1
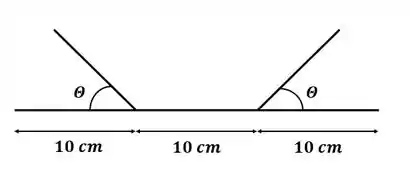
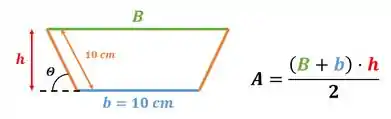
Fala aí, pessoal! Todos prontos para mais um exercício de encontrar o Ponto Máximo? Vamos começar imaginando essa calha, o formato é de um trapézio com um comprimento indefinido:
O enunciado nos pede o ângulo para máximo para que a capacidade de carregar água seja máxima, logo estamos falando sobre o VOLUME!
O Volume da calha nada mais é do que o produto da área pelo comprimento da calha:
Você concorda comigo que o comprimento não vai mudar com o ângulo de abertura dado no enunciado? Então podemos analisar apenas a área trapezoidal da nossa calha e pensar no ângulo que torna essa área máxima:
Passo 2
Vamos olhar com carinho para essa área agora:
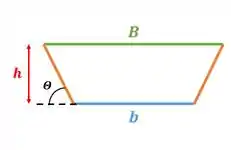
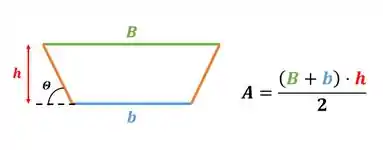
Como estamos falando de um trapézio, temos uma base menor , uma base maior e a altura . Além disso o enunciado nos disse que com a horizontal, os lados do trapézio formam um ângulo tanto de um lado quanto de outro. Logo a fórmula da área do trapézio pode ser escrita como:
Como o enunciado também nos disse, tanto a base menor quanto as laterais do trapézio que foram dobradas medem :
Olhando com mais atenção para o triângulo formado entre a altura, o lado dobrado e o ângulo :
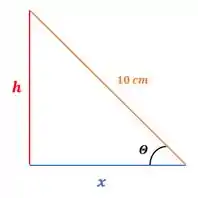
Podemos encontrar uma relação entre os valores de , e o lado dobrado :
Além disso também podemos encontrar uma terceira distância que vamos chamar de :
Você ta me perguntando pra que vamos usar o valor de , mas eu já vou te mostrar!
Lembra a fórmula da área do trapézio:
Nós já sabemos o valor de , acabamos de descobrir o valor de , mas ainda não sabíamos o valor de . Agora olha comigo para esse desenho aqui:
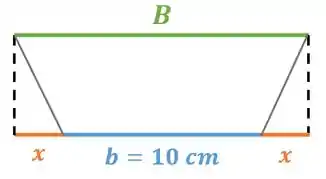
Veja se você concorda comigo, é a soma de com aqueles dois pedacinhos, onde cada um mede :
Passo 3
Nossa área do trapézio é:
Substituindo:
Podemos simplificar, colocando o termo em evidência:
Para encontrar o valor de que maximiza a função da área, precisamos derivar essa função em relação a :
Utilizando a regra da derivada do produto:
Encontramos:
Lembrando da relação trigonométrica:
Logo:
Substituindo:
Encontramos então uma função do segundo grau, onde normalmente vemos o , dessa vez estamos vendo :
Passo 4
Para encontrar o ponto de máximo, da função da área, precisamos igualar a derivada a zero:
Percebemos que temos uma equação de segundo grau igual a zero:
Então podemos usar Bhaskara para resolver:
Temos duas possibilidades:
Vamos encontrar os ângulos:
Substituindo os valores de cossenos que nós encontramos através de Bhaskara:
Então:
Analisando essas duas respostas, podemos ter um ângulo de 180°? Não, porque esse ângulo não permitiria ter a área do trapézio. Logo, nosso ângulo de abertura que maximiza a capacidade da calha de carregar água é o ângulo de .