Determine o retângulo de área máxima, e lados paralelos aos eixos coordenados inscritos na elipse de equação
Passo 1
Antes da gente partir pras contas, vamos visualizar o que a questão pede. Como temos uma elipse, se reescrevermos a equação:
Vemos que essa é uma elipse de centro com semieixo vertical igual à e semieixo horizontal igual à . Esboçando, temos:
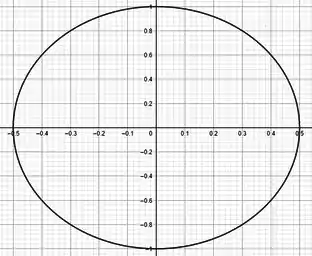
Queremos um retângulo inscrito nessa elipse, de lados paralelos ao eixo. Beleza, vamos desenhar:
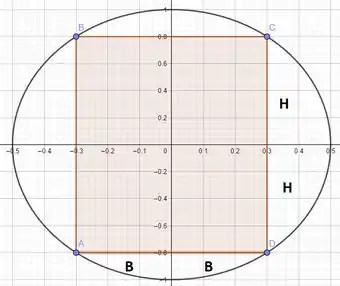
Pela simetria do problema, vamos chamar a altura desse retângulo de e a base de . Sendo assim, a área desse retângulo vai ser:
E olha só, queremos achar o retângulo de maior área, então é exatamente a função que queremos otimizar! Mas bem, ela do jeito que tá não resolve nada porque não vamos ter como uma função de uma única variável. Vamos modelar então !
Passo 2
Pra modelar vamos olhar só o primeiro quadrante do plano. Assim enrola menos a nossa cabeça:
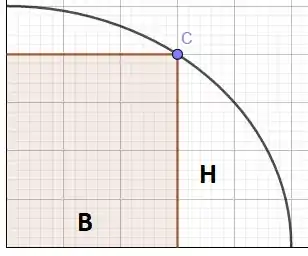
Vamos pensar no primeiro, veja que quando eu quero um retângulo no primeiro quadrante que tenha base igual à , vamos ter . E ainda, que quando queremos que esse retângulo acima tenha base , vamos ter :
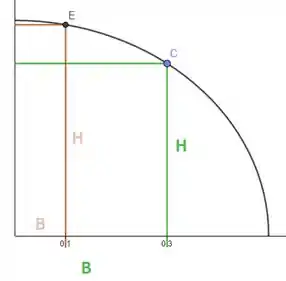
Opa, já que é assim então, vamos ter
Agora vamos tentar escreve . Dá uma olhada na imagem acima, toda vez que mudamos mudamos também, mas sempre tem o tamanho igual à altura da curva naquele ponto ! Sendo assim, como a parábola é:
Isolando :
Como estamos falando do primeiro quadrante, , e logo a altura da curva é dada por:
E se é a altura da curva, vamos ter:
E fechamos a modelagem! A área desse retângulo vai ser:
Passo 3
Agora que ta modelado, é só a gente por a mão na massa. Queremos achar o que maximiza . Então bora derivar e igualar à pra procurar os pontos críticos dessa área:
Igualando à :
Mas como só estamos olhando o primeiro quadrante, não vamos nem considerar valores negativos. O único ponto crítico pra gente checar vai ser:
Mas será que ele vai ser um ponto de máximo mesmo? Vamos ver. Escolhendo um pon to antes desse, como por exemplo, , bora checar o sinal da primeira derivada:
E checando um ponto um pouco depois, como por exemplo, temos:
E veja só! Como a primeira derivada dá a inclinação da reta tangente, se antes a função era crescente (inclinação positiva) e depois é decrescente (inclinação negativa), então de fato:
É um ponto de máximo! Sendo assim, calculamos as dimensões de área máxima fazendo:
Como o retângulo grande tem altura e base , fechamos a questão multiplicando os resultados acima por :