Forma-se um triângulo retângulo no primeiro quadrante com vértice na origem e no qual a hipotenusa é um segmento de reta tangente ao gráfico de , cujas extremidades estão sobre os eixos coordenados.
Existe uma área máxima para tal triângulo? Existe uma área mínima? Justifique.
Qual o comprimento da menor hipotenusa desta família de triângulos? Certifique-se de que sua resposta dê o mínimo global.
Passo 1
A gente tem que começar a questão sempre desenhando o esquema do que acontece na situação pedida. Estamos trabalhando no primeiro quadrante com o gráfico , de modo que uma reta tangente ao gráfico que intercepta os dois eixos coordenados é a hipotenusa do triângulo retângulo que tem vértices nos interceptos e na origem.
Se chamarmos o ponto de tangência com de , teríamos o seguinte:
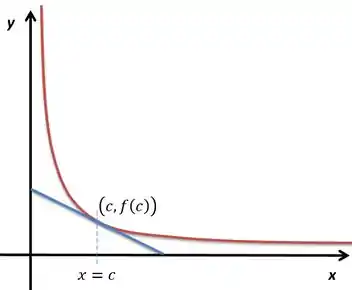
Tendo em vista o nosso triângulo delimitado pela reta azul e os eixos vamos achar uma fórmula para sua área. Primeiro, a equação da reta modelada por teria um coeficiente angular que seria igual à derivada de em :
Assim, se a reta passa no ponto temos que:
A reta é dada por
Passo 2
Bom, a reta toca o eixo quando e o eixo quando . Portanto, a gente pode descobrir a distância da origem aos interceptos:
Reescrevendo no desenho, temos isso:
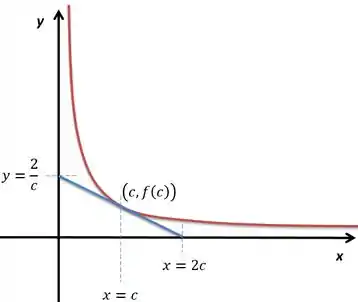
Repara que é como um triângulo de base e altura . Repara, por definição a área será:
Ou seja, a área é constante para qualquer , o que significa que não existe nenhuma área máxima ou mínima!
Passo 3
Agora queremos o comprimento da hipotenusa. Por Pitágoras, ficaria:
Vamos então derivar em relação a e igualar o termo a para descobrir os pontos críticos da função:
Como trabalhamos só no primeiro quadrante do eixo real, temos:
Agora temos que provar que esse é um mínimo global. Ora, na derivada vemos que o termo será sempre positivo no intervalo . Dado isso, vemos que o dita o sinal da derivada e, para dentro do intervalo o termo será negativo. Para o intervalo vemos que a derivada é sempre positiva. Dito isso, se antes de o gráfico é sempre decrescente e depois sempre crescente, sem que haja qualquer descontinuidade no intervalo , é um mínimo global dentro do mesmo intervalo!
Dado isso, calculamos :