UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 3.5a
Se um objeto de massa m é solto a partir do repouso, um modelo para sua velocidade v após t
segundos, levando-se em conta a resistência do ar, é
onde g é a aceleração da gravidade e c é uma constante positiva. (a) Calcule
Qual o significado desse limite?
Passo 1
Eaew, belezinha?
A questão nos pede para calcular o limite da velocidade de um objeto que sofre resistência do ar no seu movimento a partir do repouso. Sabemos que, para um objeto em queda livre sujeito apenas a força da gravidade, a velocidade do objeto aumenta linearmente com o tempo pois v = gt. Mas o nosso caso aqui é um pouco diferente: o corpo não está sujeito apenas à força da gravidade, então sua velocidade não aumenta linearmente com o tempo. Para instantes de tempo pequenos, vemos que a resistência do ar reduz significativamente a velocidade do objeto. No entanto, sua velocidade vai aumentando com o passar do tempo. Mas o que ocorre depois de um tempo suficientemente grande? Para descobrir isso precisamos verificar o comportamento da função exponencial no limite em que seu argumento vai à . Bora dar uma olhada no gráfico da função então!
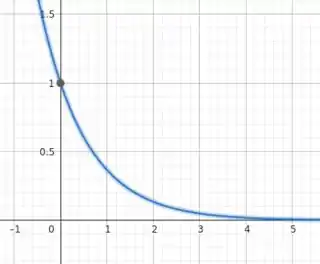
Passo 2
Do gráfico da função exponencial com argumento negativo, vemos que, quando t é muito pequeno, a função é bem próxima de 1, o que faz com que a velocidade inicial do objeto seja muito pequena. No entanto, conforme o tempo passa, a exponencial diminui rapidamente, indo à zero no limite de . Assim, nesse limite, temos que a função v(t) será aproximadamente constante, visto que o termo irá à zero. Assim, a diferença
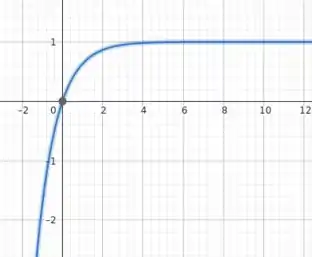
Uma outra maneira de ver que a velocidade tende à um valor constante no infinito é notar que e, quanto maior for o t, maior será o denominador da expressão, de modo que, no limite de t infinito, esse termo se torna desprezível para a velocidade. Então, depois de um tempo significativamente grande, o objeto cai com velocidade aproximadamente constante, e portanto, um movimento aproximadamente uniforme, o que é um comportamento bem diferente da queda livre. Dá uma olhada num gráfico qualitativo da velocidade do objeto com o passar do tempo:
A velocidade se torna aproximadamente constante!