Um oleoduto tem a forma de curva com , e medidos em quilômetros. Será construída uma cerva tangente à curva no ponto . Determine as coordenadas do ponto de modo que a área da região triangular formada pela cerva e pelos eixos seja mínima.

Para variar, vamos começar desenhando a figura, né? Meu oleoduto é a parábola em vermelho e a reta azul é a tangente que passa em .

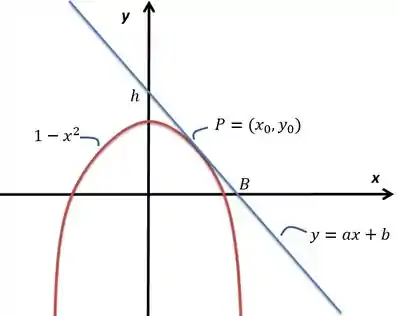
Ok, a partir daqui temos que analisar as características dessa reta e, então, minimizar a área que essa reta forma com os eixos e . Repara também que a análise tá restrita ao quadrante, já que ele disse que o oleoduto vai só de até , e que a área desse triângulo que nos interessa é:

Ok, e como minimizar essa área? Temos que escrevê-la em uma só variável, mas até lá vamos ter que pensar sobre essa reta, o que já sabemos dela. Bom, se ela é tangente ao

Nós sabemos que seu coeficiente angular será dado por , onde esse é justamente o do ponto .

Nesse caso, , então . E o b? Bom reta passa pelo ponto com , correto? Nesse caso, podemos substituir esse ponto na equação da reta e matar o :

A reta, enfim, é dada por ! Tranquilo, mas como eu tiro dessa reta os valores de e ? Lembra que essas medidas são dadas quando a reta toca os eixos, ou seja, onde e onde , respectivamente!

Então, vamos escrever nossa área em função do , do ponto :

Agora sim! Temos uma função de uma variável que podemos derivar e, dessa forma, minimizar.

A outra coordenada, o , a gente acha pela função:

Assim, !