Se um objeto dista unidades de um foco de intensidade luminosa constante , a luminosidade do objeto é igual a . Dois focos, e com intensidades e , respectivamente, encontram-se separados por unidades. Em que ponto do segmento de reta liga a , a luminosidade é mínima? Qual deve ser a razão entre e para que o ponto de luminosidade mínima entre os dois focos esteja a uma distância de unidades da fonte de luminosidade ?
Passo 1
Bom, se imaginarmos que a intensidade luminosa num ponto é igual a soma de toda intensidade incidente nela teremos que a intensidade num ponto qualquer entre será:
Esquematizando a figura, teríamos algo assim:
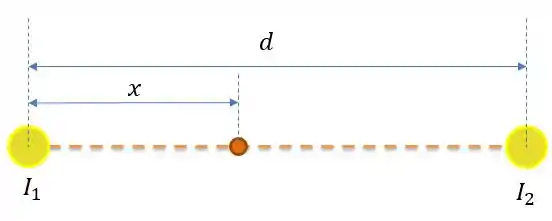
Onde, pelo enunciado:
Assim, a intensidade num ponto qualquer da reta que une as duas fontes será:
Para minimizarmos essa função devemos derivá-la e igualar a .
Passo 2
Esse é o onde a intensidade é mínima. Para provar que ele é realmente de mínimo e não máximo basta analisar que nas proximidades das lâmpadas a intensidade tende a .
Passo 3
Quanto a segunda pergunta, basta igualar esse achado a e achar a relação entre e que é gerada: