Se um retângulo tiver sua base em um eixo e dois vértices sobre a curva . Mostre que o retângulo tem maior área possível quando os vértices estão nos pontos de inflexão da curva.
Passo 1
Tá bem, vamos primeiro esboçar o problema. A curva é uma exponencial no expoente sempre negativo e se comportará sempre como a parte à esquerda da origem de , ou seja, se aproximando de zero:
Como a base está no eixo e os outros dois vértices estão sobre a curva, teremos:
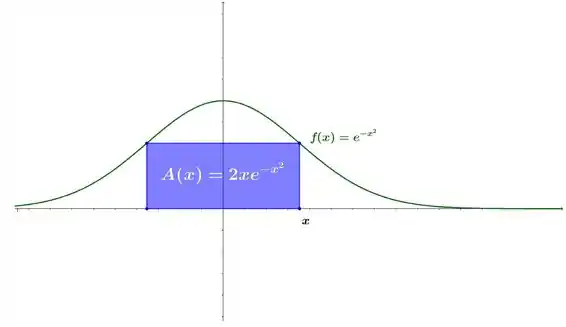
Passo 2
Vamos tentar atribuir variáveis ao problema e relacioná-las agora. Como temos um retângulo de base (à esquerda e à direita da origem) e altura a área será:
Show, queremos mostrar que o valor máximo dessa área é um ponto de inflexão, ou seja, ocorre quando a figura muda de concavidade.
A relação entre os dois pode ficar um pouco confusa, então vamos determinar esse ponto de máximo otimizando e depois verificamos se trata de um ponto de inflexão.
Passo 3
Para otimizar, achamos os pontos críticos que, nesse caso, ocorrem quando a derivada é zero. Derivando pela regra do produto e cadeia:
Como é uma função composta, para derivar, consideramos que é o que está na exponencial e, então teremos:
Sendo:
Ficando:
Temos que igualar isso a zero agora:
Como para todo , então resta:
Desconsiderando a parte negativa, pois é uma unidade de medida para área.
Passo 4
Vamos verificar agora se é um ponto de máximo global da área. Para tal, temos que, para , por exemplo:
Como a derivada é maior que zero à esquerda e menor que zero à direita de , então, pelo teste da primeira derivada, esse é um ponto de máximo.
Para os extremos temos:
Aplicando L’Hôpital:
Logo, esse é um ponto de máximo global mesmo.
Passo 5
Agora só resta verificar se é um ponto de inflexão mesmo. Para isso, vamos derivar novamente. Pela regra do produto:
Show, agora vamos verificar se faz :
Opa, reparem que não deu igual a 0 , logo não é um ponto de inflexão
Resposta
Máximo para que não é um ponto de inflexão.