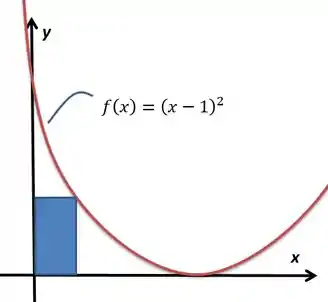
Dentre os retângulos limitados pelo eixo , pelo eixo e pelo gráfico de definida por (conforme a figura), determine as dimensões do retângulo de área máxima.
Passo 1
Bom, a área desse retângulo é dada pela base vezes a altura. No caso, a base é a distância horizontal entre o ponto do gráfico e o eixo , que acaba sendo mesmo. Já a altura é dada por , o que nos faz concluir que a área é dada por:
Passo 2
Para otimizá-la vamos derivar a área em função de e igualar o termo a . Como é um polinômio, ela vai sempre existir.
Por Bhaskara, temos que as raízes serão:
Como vemos, ao substituir na função teríamos uma área nula:
Para saber se é um ponto de máximo mesmo, devemos testar o sinal da derivada. Como é fácil de derivar, podemos usar o teste da segunda derivada.
Como a segunda derivada é negativa no ponto crítico, podemos concluir que o responsável pelo retângulo de área máxima é .
É um ponto de máximo global, pois no outro ponto crítico, que a fronteira direita, a área é nula. No ponto , que é a fronteira à esquerda:
Uma vez que é a base do retângulo e a sua altura, descobrimos:
Essas são as dimensões do nosso retângulo, !