Problemas de Otimização
Dentre todos os retângulos do plano com centro na origem, lados paralelos aos eixos coordenados e inscritos na elipse
determine aquele de maior perímetro.
Passo 1
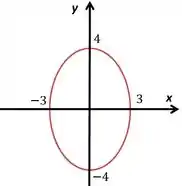
O elipse vai ficar algo assim, considerando os pontos onde toca os eixos:
Centrando um retângulo na origem que toque simetricamente em pontos da elipse, ficaria algo assim:
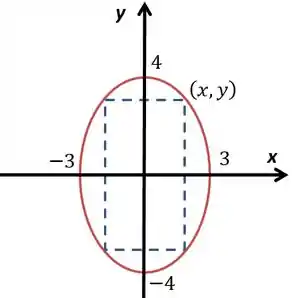
Assim, por simetria, é como se o perímetro fosse vezes o a soma dos lados do retângulo do primeiro quadrante, que tem base valendo e altura valendo , ou seja:
Porém, como o ponto pertence à elipse, temos que pode ser dado em função de :
Passo 2
Vamos derivar a área em função de e igualar a para otimizar a função:
Usando uma regra da cadeia, temos:
Multiplicando tudo por , ficamos com:
Elevando os dois lados ao quadrado:
Colocando todo mundo no mesmo denominador:
Como estávamos trabalhando inicialmente no primeiro quadrante, o que otimiza a função é .
Passo 3
Para garantir que esse é um ponto de máximo, basta resolver a mesma equação acima, só que colocando e no lugar do . Notaremos que a derivada é positiva antes de e negativa depois, o que significa que esse é um ponto de máximo!!
Assim, o maior retângulo centrado na origem e com seus vértices na elipse é aquele de lados: