Determine o retângulo de área máxima e lados paralelos aos eixos coordenados, inscrito na elipse
Passo 1
Vamos tentar esboçar o problema. Queremos um retângulo inscrito na elipse, que estará mais na forma:
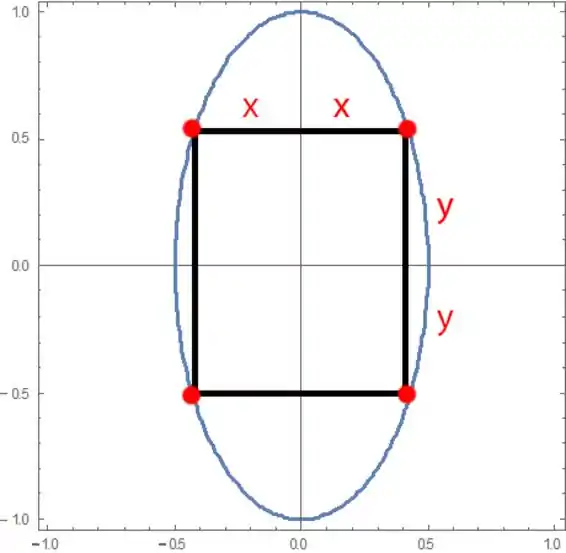
Veja que os lados do retângulo valem e . O dois aparece, pois cada quarto do retângulo está em um quadrante.
Assim sendo, a área será:
Passo 2
Precisamos tentar deixar isso em função de uma única variável, para tal, recorremos a elipse:
Isolando :
Como trata-se de uma medida, pegamos somente a parte positiva e substituímos:
Passo 3
Para achar o ponto de máximo, precisamos achar os pontos críticos que, por sua vez, são encontrados derivando e achando os zeros e os pontos de inexistência. Pela regra do produto e cadeia:
A derivada passa a não existir para quando o denominador é zero, ou seja:
Temos valores negativos e positivos, mas novamente consideramos somente os positivos, pois é uma medida. Nesse ponto:
A área é zero, então esse ponto não nos interessa. Vamos ver quando a derivada é zero:
Novamente, consideramos somente a parte positiva.
Passo 4
Precisamos agora testar se esse ponto é um ponto de máximo. Para isso, aplicamos o teste da primeira derivada, escolhendo um ponto à esquerda e à direita. Temos que tomar cuidado para não passar de outro ponto crítico nessa hora para não obter alguma informação errada. Vamos escolher então:
Substituindo esses pontos na derivada:
Como a derivada é positiva à esquerda e negativa à direita, é, de fato, um ponto de máximo.
Passo 5
Substituindo o ponto de máximo:
O valor de cada lado será:
E:
Ufa!