Determine as dimensões do retângulo inscrito no semicírculo de raio e que tem o maior perímetro. Justifique sua resposta.
Passo 1
Entender o problema
Se você sentiu cheiro de questão de otimização quando leu esse enunciado, sentiu certo! A questão pode até parecer confusa, mas se a gente der uma esboçada nos gráficos das cruvas, fica tranquilo de entendermos. Da uma olhada:
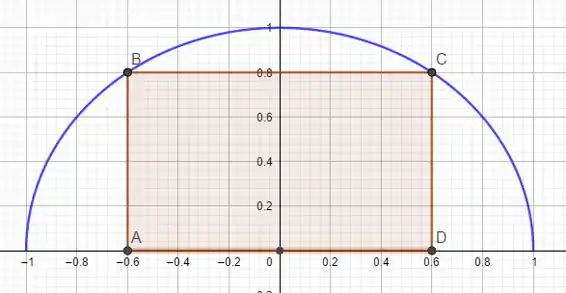
O que a questão pede é para maximizarmos o perímetro desse retângulo e acharmos as dimensões do retângulo pra essa área! Pra fazer isso, precisamos primeiro de um jeito de escrever:
Show de bola, sabendo como o perímetro varia com , achar o maior perímetro vai ser mel na chupeta: basta derivar e igualar a ! Pra que sinais de negativo não nos enrolem, vamos resolver o problema dessa forma aqui:
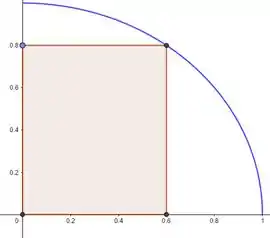
Esse perímetro vai ser então metade do perímetro do retângulo original, se descontarmos o lado esquerdo desse retângulo. Chamando esse perímetro de , vamos ter que:
E como com oestamos falando do perímetro de um retângulo, o pulo do gato pra resolver essa questão vai ser encontrar como a altura varia com , isto é, e como a base varia com , isto é, . Isso porque o perímetro (de novo pra não esquecer: descontando o lado esquerdo) de um retângulo é a soma dos lados. Sendo assim:
Passo 2
Encontrar a expressão de e
Pra sabermos a expressão de temos que encontrar esses dois primeiro, não é mesmo? Então vamos lá! Começando pra base:
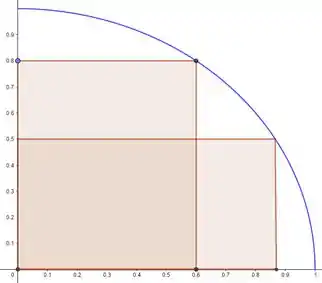
Opa, se quando a base tem tamanho e quando a base tem tamanho então a base vai ter a expressão:
Agora, sobre a altura:
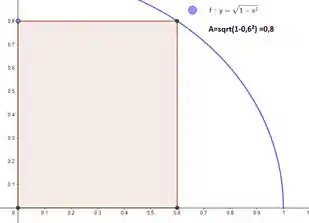
Quando , a altura é igual a . E da uma olhada no gráfico: o que é isso se não ? A expressão de a gente tira de:
Mas como estamos considerando só a parte de cima do círculo, tiramos o sinal de degativo e ficamos com:
Portanto, a altura do retângulo vai ser a própria
Passo 3
Encontrar a expressão de
Agora temos tudo pra saber como a área do retângulo varia com . Partiu então:
Logo:
Passo 4
Otimizando o valor do perímetro
Opa, agora pra achar o valor de que maximiza o perímetro, basta achar o que satisfaz . Vamo que vamo:
Mas como dividimos o problema pela metade pra não precisarmos nos preocupar com valor negativos, vamos usar
Pra esse valor então a altura vai ser:
E a base do retângulo original vai ser:
O perímetro máximo vai ser então: