Um quadro de altura está pendurado em uma parede vertical de modo que sua borda inferior está a uma altura do raio de visão horizontal de um observador. A que distância da parede deve colocar-se o observador para que a sua posição seja a mais vantajosa para contemplar o quadro, isto é, para que o ângulo de visão seja máximo?
Passo 1
Agora que chegamos até aqui, vamos diluir os passos e ser mais diretos na resolução.
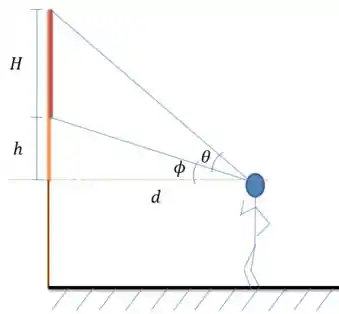
Vou esboçar então o que a questão pede, onde o pedaço em vermelho é o quadro e em laranja essa distância ao chão, com o ângulo de nome .
Passo 2
Olha o que dá para dizer se eu chamar aquele ângulo de visão da parte inferior do quadro com a horizontal de e a distância da pessoa que vê o quadro horizontalmente ao quadro de .
Não sei se você vai lembrar, mas existe uma fórmula relacionando soma de tangentes. É essa aqui:
Se eu somar as tangentes de e de eu vou achar uma expressão que me trará a cara da tangente de . Tendo ela posso procurar um meio de otimizar esse .
Passo 3
Vamos lembrar uma coisa, a questão pede para encontrarmos a distância que gera o maior ângulo de visão. Logo, é como se tivéssemos que achar um e, a partir dele, descobrir em o que gera o maior . Enfim, podemos fazer isso implicitamente, já no formato que está aqui em cima, com o detalhe que deve ser no ponto em questão.
Essa é a nossa distância, em termos das alturas!