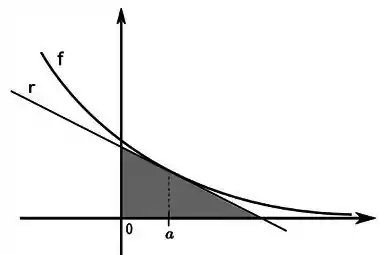
Um triângulo retângulo, localizado no primeiro quadrante, tem um vértice na origem e seus outros dois vértices determinados pela interseção da reta tangente ao gráfico da função com os eixos coordenados (ver figura).
Determine a equação da reta tangente ao gráfico da em .
Determine as interseções da reta com o eixo e com o eixo .
Determine o valor de de forma que a área do triângulo seja máxima, considerando somente os triângulos formados no quadrante.
Passo 1
Vamos modelar uma reta , (não usei para não confundir com o ). Sabemos que seu coeficiente angular é igual a em .
Sabemos ainda, porém, que a função da reta passa pelo ponto quando , ou seja, passa pelo ponto . Assim descobrimos o :
Enfim, concluímos a nossa reta:
Passo 2
Suas interseções com os eixos e acontecem em e respectivamente:
Passo 3
Pela figura inicial percebemos que o triângulo tem como dimensões de altura e base as interseções com os eixos e , respectivamente. Logo, sua área será:
Para achar a área máxima devemos derivar a função em relação a e igualar a expressão a . Ela vai sempre existir, pois a o denominador é sempre maior que zero.
Como o triângulo deve ser formado no primeiro quadrante, é o único valor que nos serve. A gente observa que e , o que garante que é ponto de máximo e não mínimo, dado que é o único máximo em .