Problemas de Otimização
Sejam . Determine, caso exista, o perímetro mínimo dos triângulos de base e altura (relativa à base dada) .
Passo 1
Ora, Vamos desenhar o que seria um esboço da questão:
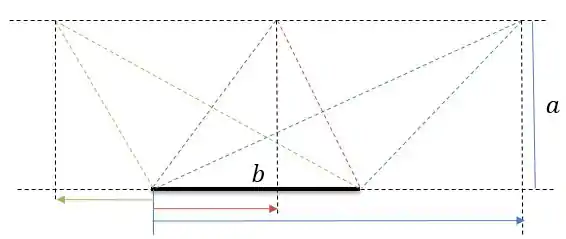
Nesse desenho tentei englobar todas as possibilidades dos triângulos trabalhados. Para o triângulo azul, que tem um ângulo obtuso na direita, se chamássemos a distância da seta azul de uma variável nosso perímetro seria:
Se pegássemos o vermelho, com os três ângulos agudos e sendo a distância representada pela seta vermelha, o perímetro seria:
Como percebemos, o triângulo vermelho é similar ao caso azul, então não precisamos representá-lo novamente, já que são parecidos. Como temos que é igual a , podemos generalizar a nossa fórmula do perímetro por:
Passo 2
Vamos derivar a função e igualá-la a para que possamos otimizar a função:
Logo, Quando temos o menor perímetro, já que observamos que à medida que o ponto de altura se afasta da base o perímetro vai aumentar indefinidamente, já que as distâncias tenderiam a . Vamos descobrir quanto valeria o perímetro: