Encontre a maior área de um retângulo que podemos inscrever entre o gráfico da função e o eixo das abscissas . Justifique por que o retângulo que você encontrou será o de maior área.
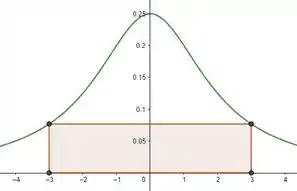
Passo 1
A questão ta pedindo pra gente achar a maior área, certo? Oras, então podemos chamar essa questão de uma questão de otimização: achamos a área, e otimizamos pra achar a maior possível! E o que é a área de retângulo se não a sua base vezes a sua altura?
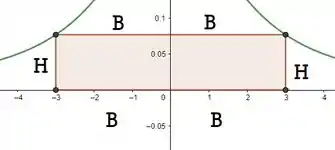
Ok, mas e agora? Não dá pra otimizar isso! Caaaalma gafanhoto, não dá porque não relacionamos as variáveis ainda! E é exatamente isso que vamos fazer agora!
Passo 2
Vamos brincar um pouco com o valor de . Perceba que, quando eu quero que valha , temos e quando eu quero que valha , tenhos !
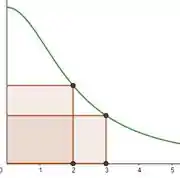
Opa, então é o próprio ! Escrevemos então:
Agora vamos checar o valor de . Veja só, se eu escolher , a altura vai ser uma reta que sai da horizontal () e vai até a função, isto é . E, analogamente, se eu escolher , a altura vai ser uma reta que sai da horizontal e vai até .
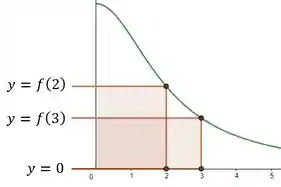
Oras, então sai ser ninguém menos que a própria função do enunciado!
Peraí, quer dizer que tanto quanto são funções de ? Isso mesmo! E se são, conseguimos relacionar as variáveis e escrever a área também como uma função de ! Dá uma olhada:
Passo 3
Beleza, temos a função a ser otimizada! Agora pra achar a área máxima, basta achar o ponto de máximo de , tranquilo? E que melhor forma de fazer isso do que derivando e achando os pontos críticos! Bora lá:
Igualando à pra achar os pontos críticos, temos:
Mas como e não existe base com valor negativo, o único que vale é:
Show de bola, achamos o ponto que maximiza a área! Se isso ocorre quando , temo então:
Passo 4
Pra gente fechar a questão com chave de ouro, falta só a gente confirmar que o ponto achado é um ponto de máximo global. Pra isso, vamos olhar a cara de :
Perceba que para temos e que para temos . Ou seja, só podemos colocar aí nessa função valores positivos de porque se não teríamos áreas negativas ou nulas, o que não dá muito certo aqui!
Agora, dá uma olhada ainda nesse limite:
Realizando L’Hospital:
Não é que a função decresce no infinito? Então, se saímos de uma área nula quando , crescemos até a área quando e quando a área volta a ser nula, realmente a maior área possível é !