Um contêiner retangular sem tampa para estocagem deve ter volume de O comprimento de sua base é o dobro de sua largura. O material para a base custa e o material para as laterais custa . Encontre o custo dos materiais para o barato desses contêiners. Não esqueça de verificar que de fato esse é o mais barato dos contêiners!
Passo 1
Desenhar e entender o problema
Show de bola, vamos lá! Pra começar, vamos desenhar esse contêiner:

Tem que desenhar assim mesmo na prova se não o professor não entende. Finge que esse contêiner está aberto, ok? Pois bem, o enunciado diz que comprimento de sua base é o dobro de sua largura. Sendo assim, temos:

O enunciado também nos dá o volume. Como
Vamos ter:
Opa, sabemos agora como cada um dos comprimentos varia com . Guarda isso porque vamos precisar
Passo 2
Calcular o preço de cada face
O pulo do gato pra entender isso aqui é ver a unidade de medida: o preço é dado por área! Sendo assim, a soma das áreas vai ser:
Onde os dois primeiros são termos referentes as 4 laterais e o último a base. Sendo o preço da base diferente do preço das laterais, gente consegue mole o preço total multiplicando a área pelos preços individuais. Sendo assim:
Mas como:
O preço total, em função de , vai ser:
Passo 3
Otimizar o preço total
Como ninguém gosta de gastar a toa, a ideia agora vai ser otimizar esse preço. Ou seja, achar o valor de que minimiza o preço total. E o que é isso se não o clássico “deriva e iguala a ” ? Partiu então:
Ou seja, basta a gente resolver:
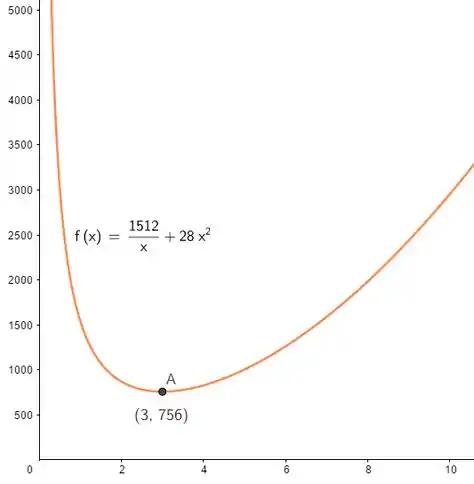
Então o menor preço vai acontecer quando . Em reais, vamos ter:
E só pra fechar com chave de ouro e ficar bonitinho, dá uma olhada no gráfico de :