Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Otimização – Modelagem

Ver Teoria
Exercício 5123467891011121314151617181920212223242526272829303132333435363738394041424344454647

Enunciado

Problemas de Otimização

Considere a elipse de equação x 2 25 + y 2 9 = 1 e todos os triângulos retângulos construídos com um dos vértices em ( 5,0 ) , um sobre a elipse e o terceiro sobre o eixo O x , como na figura abaixo. Justifique a existência, dentre esses triângulos, de um com área máxima e determine as medidas de sua base e sua altura.

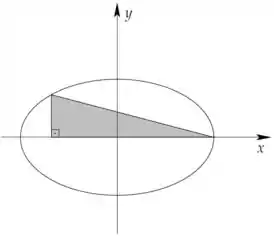
Passo 1

Olhando para os três pontos, como eu poderia descrevê-los? Um já é dado, ( 5,0 ) . Olhando para os outros, teríamos um que pertence ao eixo x que pode ser descrito então por ( x , 0 ) . O terceiro ponto é aquele que pertence à equação da elipse estando necessariamente acima desse ponto do ( x , 0 ) , ou seja, ( x , y ) onde y está em função de x através da equação:

  x 2 25 + y 2 9 = 1

y 2 9 = 1 - x 2 25

y = 9 - 9 x 2 25    

( c o m o   s ó   t r a b a l h a   c o m   y   p o s i t i v o ,   n ã o   c o l o q u e i ± )

Bom, sabendo disso eu preciso descrever a área do triângulo que está aí. O produto dos módulos dos catetos dividido por 2 me garante já essa área. E qual é o módulo de cada cateto? O que está deitado sobre o eixo x pode ser dado pela diferença entre os pontos no eixo.

5,0 - x , 0 = ( 5 - x , 0 )

Cujo módulo é o próprio ( 5 - x ) . O mesmo para o cateto vertical, diferença entre os pontos:

x , y - x , 0 = ( 0 , y )

Cujo módulo é y mesmo. Daí, escrevemos:

A = ( 5 - x ) y 2 = ( 5 - x ) 9 - 9 x 2 25 2

Passo 2

Devemos derivá-la e igualá-la a 0 para buscar pontos críticos. Usamos a Regra do Produto:

A ' x = 5 - x ' 9 - 9 x 2 25 2 + 5 - x 9 - 9 x 2 25 ' 2

= ( - 1 ) 9 - 9 x 2 25 2 + 5 - x - 9 x 25 9 - 9 x 2 25 2

Igualando a 0 teremos isso:

- 1 9 - 9 x 2 25 2 + 5 - x - 9 x 25 9 - 9 x 2 25 2 = 0

5 - x - 9 x 25 9 - 9 x 2 25 = 9 - 9 x 2 25

- 9 x 5 + 9 x 2 25 = 9 - 9 x 2 25

- 5 x + x 2 = 25 - x 2

2 x 2 - 5 x - 25 = 0

x - 5 x + 5 2 = 0

x = 5

x = - 5 2

Passo 3

Pelo desenho, vemos que visualmente a área quando x = 5 será 0 (área quando os três pontos estariam coincidentes no ponto ( 5,0 ) ). Sabendo que dali até x = - 5 2 a área cresceu e depois diminuirá até zerar de novo (quando x = - 5 a área será 0 também) sabemos que o ponto crítico em questão é um ponto de máximo. Senda assim, basta achar as medidas do triângulo:

B a s e : 5 - x = 5 - - 5 2 = 15 2

A l t u r a :   9 - 9 x 2 25 = 9 - 9 5 2 2 25 = 9 - 9 4 = 27 4 = 3 3 2

Á r e a   m á x i m a : 15 2 3 3 2 2 = 45 3 8

Resposta

B a s e : 15 2   ;   A l t u r a :   3 3 2   ;   Á r e a   m á x i m a : 45 3 8

Exercícios de Livros Relacionados

Estão dados os gráficos da função posição de dois corredores, A e B que correm 100 metros rasos e terminam empatados.Descreva e compare como os corredores correram a prova.Em que instante a distância
Se a meia-vida do rádio for de 1.690 anos, que porcentagem da quantidade presente agora restará após:a) 100 anos?
Nos exercícios de 40 a 45, uma partícula está se movendo ao longo de uma reta, de acordo com a equação de movimento dada, onde s cm é a distância orientada entre a partícula e a origem no instante t s
Encontre (d^3 y)/(d x^3) se y = sqrt(3 - 2 x) .
Um objeto está escorregando por um plano inclinado de acordo com a equação s = 12 t 2 + 6 t , onde s m é a distância orientada do objeto até o topo do plano, após t s do início do movimento. (a) Ache