3) Um retângulo tem os dos vértices inferiores sobre o eixo e os dois vértices superiores pertencentes à curva . Dentre todos os retângulos nestas condições, quais as dimensões daquele que tem a maior área? Justifique sua resposta!
Passo 1
Olha só galera, pra entender direitinho essa questão, um bom primeiro passo é fazer um esboço rápido desse retângulo e dessa curva. Como a curva é uma parábola com o termo multiplicativo de negativo, vamos ter um caso como esse aqui:
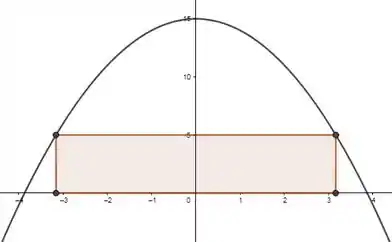
Como queremos otimizar a área, achando a maior possível, temos que primeiro montar a equação da área. Show! Pra gente não se enrolar com números negativos, recomendo olhar somente pra esse lado:
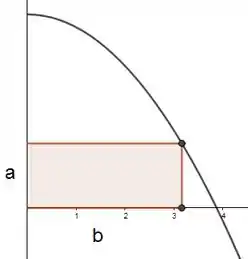
Opa, dessa forma fica tranquilo de entender que a área vai ser:
Uma vez que a figura acima é só metade da área do retângulo original. Pra otimizar, no entanto, vai faltar pra gente relacionar as variáveis , pra que seja uma função de uma variável só.
Passo 2
Pra relacionar as variáveis direitinho, olha de novo pra essa figura:
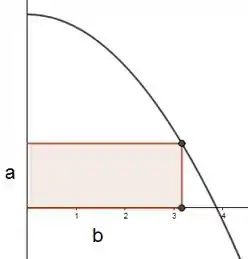
Pô, se eu escolho um valor qualquer de , o meu vai sair sempre do eixo , em uma altura , e tocar a curva! Dessa forma, temos que:
E pronto! Ta montada a fórmula da área! Se e , então e tem a expressão:
Passo 3
Agora pra fechar, vamos lembrar que, como toda boa otimização, pra gente achar o ponto de máximo, precisamos derivar e igualar a zero! Sendo assim:
Como é uma unidade física de meio valor de base, o valor negativo não rola, não é mesmo? Então o valor de que otimiza essa função é:
Antes da gente enunciar as dimensões, vamos checar se esse ponto é de máximo mesmo, testando o sinal da primeira derivada em pontos antes e depois. Podemos por exemplo, usar e :
Se antes a função era decrescente (porque tem primeira derivada positiva) e depois passou a ser decrescente (porque tem a primeira derivada negativa) então tá certíssimo! é de fato um ponto de máximo. E como as dimensões do retângulo são:
O retângulo de maior área será: