Q03) Deseja-se construir um reator nuclear em uma usina elétrica. O reator tem formato cilíndrico e será instalado dentro de uma cúpula semi-esférica de raio igual a , conforme ilustra a figura abaixo. Determine o raio da base do cilindro de maior volume que pode ser instalado dentro da cúpula.
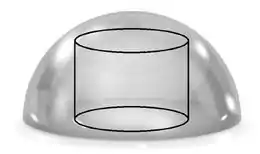
Passo 1
Vamo que vamo. A questão quer maximizar o volume, certo? Então vamos escrever ele. Sendo o volume do cilindro, temos:
Mas peraí, não da pra otimizar assim né? Tem duas variáveis! Realmente não dá! Vamos precisar relacionar as variáveis então. Pra isso, vamos parar de pensar em e vamos pro . Fazendo um corte na figura, temos:
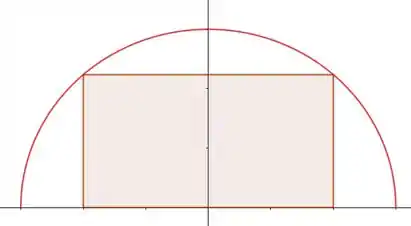
Temos então um retângulo inscrito em uma semi-circunferência que, como a equação de uma circunferência é:
Nesse caso, sendo e já que estamos trabalhando só com a parte de cima, temos:
Ou seja, conseguimos modelar a equação da curva! Pra facilitar ainda mais, como o problema é simétrico, vou dividir essa figura pela metade, e teremos:
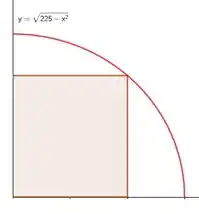
Saca só agora. Como o raio do cilindro inscrito é mutável, a figura acima não é estática. Se brincarmos de mexer o raio vamos mudar a forma desse retângulo acima, saca só:
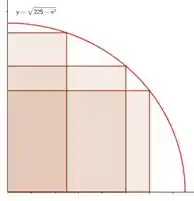
Qual a conclusão que tiramos então? É que podemos dar nome aos bois nesse retângulo:
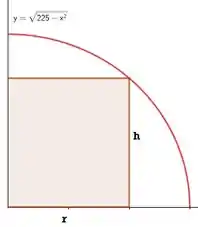
E veja bem, qualquer que tenha sido o raio que eu escolhi, ele sempre esteve sobre o eixo no exato valor de ! E pra cada raio que eu escolho, a altura é igual a uma reta que sai do eixo até a curva. E o que é isso se não a própria equação da função? Concluímos então que:
E logo a equação do volume fica:
Passo 2
Agora que montamos a função a ser otimizada, precisamos achar os pontos críticos dela. Pra isso, bora derivar em relação a então:
Colocando no mesmo denominador:
E igualando a , precisamos só nos preocupar com o numerador. Logo:
Como , então:
Passo 3
Antes de fecharmos a questão, vamos só testar as fronteiras e ver se o valor que achamos é o que maximiza mesmo o volume. Lembra que podíamos brincar de mexer com o raio?
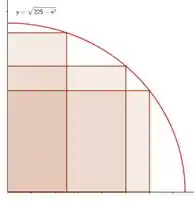
Mas não podíamos escolher qualquer um né? Tinhamos que necessariamente escolher um que estivesse entre e . Opa, então são essas as fronteiras! Testando elas na fórmula do volume:
Se parar pra pensar, geometricamente faz sentido, um raio nulo zera o volume do cilindro e um raio máximo zera a altura do cilindro! Se as fronteiras não deram em nada, então realmente:
É o valor de raio que maximiza o volume do cilindro inscrito