UFPE – Cálculo 1 – 2020.2 – Segundo Exame – Exercício 2
Uma janela normanda tem o formato de justaposição de um semicírculo sobre um retângulo. Suponha que o perímetro da janela normanda é de .
a) Determine a área da janela como função da altura do retângulo correspondente.
b) Ache as dimensões da janela com maior área possível, assim como a área desta janela (aplique os conceitos do cálculo diferencial).
Passo 1
Fala galerinha, beleza? Bora brincar um pouco com problema de otimização!
O primeiro passo desse problema é desenhar a janela normanda com retângulo de base e altura :
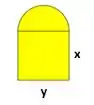
O raio do semicírculo é . A área da janela é dada por
Queremos escrever essa área apenas como função de (altura). Para isso, escrevemos que o perímetro dela é
Como , temos que
Igualando o perímetro a :
Logo,
Daí, basta substituir na expressão da área:
Passo 2
Vamos brincar um pouco com essa expressão:
Fazendo as distributivas:
Portanto,
A expressão é um pouquinho feia, mas é isso ai 😉!
Passo 3
Repare que se trata de uma função de segundo grau com concavidade para baixo (triste). Logo, essa função tem um máximo que ocorre no vértice da parábola. Derivando com relação a :
Fazendo :
Para achar o valor de :
Logo,
Ou ainda,
Portanto, as dimensões que maximizam a área da janela são