Uma página deve conter de área impressa. As margens superior e inferior devem ter , enquanto as laterais têm cada. Encontre as dimensões da página que consomem a menor quantidade de papel.
Passo 1
Observe a figura abaixo, que representa a situação descrita no enunciado.
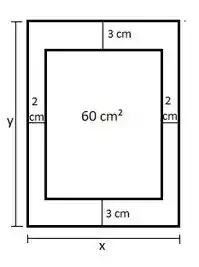
Chamaremos a altura da página de e o comprimento da página de . Queremos as dimensões da página que consome menos papel e tem área impressa de . A área impressa da página pode ser calculada pela fórmula
Nesse caso, sabemos que
Mas o que o exercício pede é a área total da página, isto é, contando com os espaços das margens. Essa área pode ser dada por
É essa que precisamos otimizar. Bora começar!
Passo 2
Precisamos que esteja em função de apenas uma variável para podermos otimizar. Então vamos isolar uma das variáveis em e depois substituir em . Vou isolar o , mas tanto faz isolar ou , você pode escolher.
Passo 3
Agora dá pra substituir na equação da área total.
Passo 4
E finalmente vamos derivar para encontrar seu ponto de mínimo.
Passo 5
Tendo a derivada, podemos encontrar os pontos críticos, igualando-a a zero.
A raiz negativa foi desconsiderada pois estamos encontrando medidas, que são sempre positivas.
Só falta descobrir se o ponto encontrado é uma mínimo da função. Analisando o sinal da derivada perto de temos que
- Antes de:
- Depois de:
Logo, de é um ponto de mínimo local.
Passo 6
Falta só descobrirmos o valor de quando . Sabemos que
e substituindo o encontramos