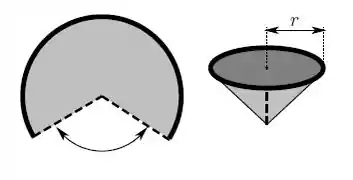
Um copo na forma de um cone é produzido cortando-se um setor circular de um disco de raio , como indicado na figura:
- Escreva o volume do copo como função do raio da base do copo
- Determine o maior volume possível desse copo
Passo 1
Enunciado enrolado né? Mas relaxa que vamos tirar de letra. Pra ficar um pouco mais claro como esse copo foi construído, que tal umas imagens? Olha o passo a passo. Primeiro, cortou o setor circular

Depois juntou as pontas e montou o cone:

Opa, fazendo isso, o que restou da circunferência, abaixo, em vermelho, é exatamente a circunferência da base do copo:
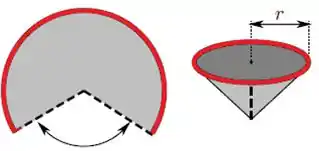
E, além disso, o raio da circunferência vira essa linha do cone, em verde:
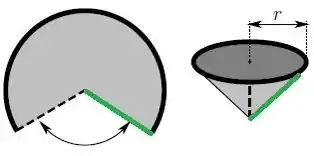
Dando nome aos bois, podemos resedesenhar o cone com linhas importantes dele nomeadas:
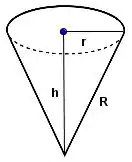
E como o volume do cone é:
Pra gente terminar de modelar essa equação em função de falta só uma coisita: achar uma expressão de em função de . Pra isso galera, dá uma boa olhada naquele zão ali. Pô, a gente sabe esse valor! Ele é exatamente a linha verde que marcamos anteriormente, que é o raio da circunferência! O enunciado deu isso pra gente! Vamos ter então:
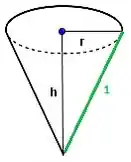
E por Pitágoras:
Juntando tudo, temos:
Passo 2
Show de bola. Agora vamos achar o maior volume. Pra otimizar, temos que derivar e igualar a zero para achar os pontos críticos, ok? Vamos ter:
Colocando no mesmo denominador:
Pra essa minah derivada zerar, a única forma possível é se o numerador zerar. Show, vamos ter então que:
Bem, pontos críticos achados. No entanto, o negativo a gente pode descartar porque raio negativo não existe. Pra saber se esse ponto crítico maximiza o volume, o jeito é calcular o volume trocando na expressão de :
Só tem mais uma coisa que temos que fazer: comparar com o valor do volume nas fronteiras. A primeira é o caso em que o raio nem sequer existe, ou seja, :
Ou seja, como por enquanto temos sim um volume máximo. Afinal, entre e o volume cresceu. Pra ser de máximo mesmo então, o volume tem que decrescer a partir de . Pra checar isso, testamos a outra fronteira, , a fronteira na qual pra a raiz no interior da fórmula de fica negativa. Belê, calculando:
E de novo temos . Como o volume cresce, chega ao seu máximo e depois volta a decrescer, o maior volume pra esse cone será: