Seja . Considere o triangulo com vértices em , e . Ache o valor de que maximize o ângulo entre e .
Passo 1
Desenhando o que está acontecendo obtemos a seguinte figura:
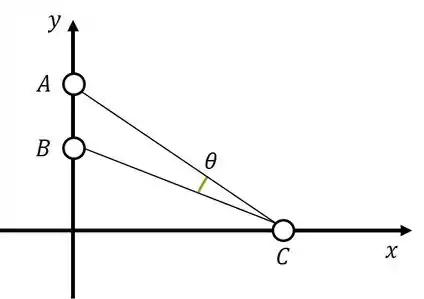
Vamos marcar um ângulo auxiliar para... hã... nos auxiliar:
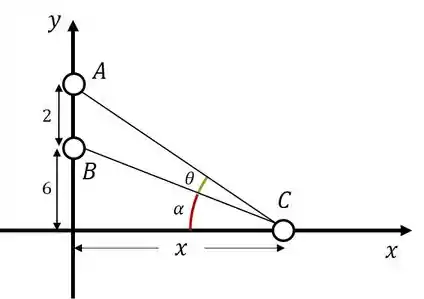
Temos então:
Passo 2
Portanto nosso ângulo desejado é:
O valor máximo é um ponto crítico onde , portanto:
Passo 3
Igualando a zero e resolvendo:
Elevando tudo à :
Sabendo, pelo enunciado, que :
Passo 4
Ou seja, achamos um ponto crítico. Agora basta provar que este ponto é máximo e é absoluto. Para provar que é mínimo sem encontrar a derivada segunda de podemos analisar como muda o sinal de sua derivada em torno de . No caso temos:
Chutando algum valor :
Portanto, como só existe um ponto crítico e nenhuma descontinuidade:
Passo 5
Chutando algum valor :
Ou seja, analogamente:
Passo 6
Ou seja, a função era crescente antes de e decrescente depois. Isto configura um ponto de máximo. Agora, se mostrarmos que a função não explode para infinito em nenhum ponto, temos que ele vai ser máximo absoluto. Como não existem descontinuidades malucas em (divisões por zero, etc.) precisamos apenas checar os extremos do domínio:
Portanto não explode para infinito em ponto algum. A função é limitada e é máximo absoluto.