Encontre dois números positivos cujo produto seja 100 e cuja soma seja mínima.

Para isso, temos que escrever em função de apenas uma variável. Como fazer isso? Usando a relação para isolar uma das variáveis.

Agora substituímos isso na função.

Para minimizar primeiro temos que achar os pontos críticos, fazendo . Então vamos derivar a função:

Agora dá pra fazer

Como o enunciado disse que os dois números são positivos, o ponto pode ser desconsiderado.

x = 10 para descobrir se ele é mesmo um ponto de mínimo. Observe que o denominador não influencia no sinal pois é sempre positive. Então basta analisar o sinal do numerador, que é a parábola cujo gráfico está representado pela figura abaixo:

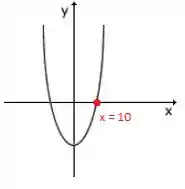
Pelo gráfico, vemos que antes de o sinal é negativo e depois de ele fica positivo. Portanto é um ponto de mínimo.

Por fim, já que temos o valor de , podemos descobrir o valor de .