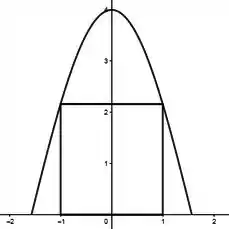
Considere a região . Determine as dimensões do retângulo de maior perímetro possível que pode ser inscrito em .
Passo 1
Opa, vamos lá. Antes da gente mergulhar na questão vamos visualizar direitinho o que tá sendo pedido: um perímetro. E o maior possível. Então temos aí uma questão de otimização! E em questões de otimização a gente precisa achar uma função a ser otimizada e uma relação entre as variáveis! Seja:
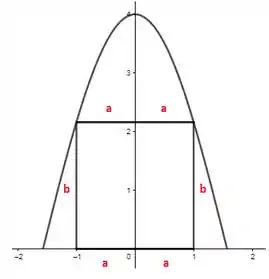
O perímetro pode ser calculado como:
E se a gente quiser só trabalhar com valores positivos pra não enrolar a cabeça, podemos fazer:
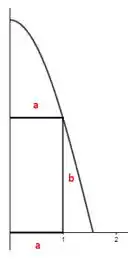
Maravilha! Falta agora relacionar e pra que seja uma função de uma variável só. Então partiu!
Passo 2
Vamos começar olhando o pro . Veja bem, quando queremos, por exemplo, que seja igual à , temos , e quando queremos que seja igual à, por exemplo, , temos que :
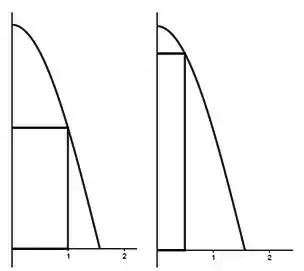
Opa, então quer dizer que ? É isso aí! Vamos ter então que:
E saca só: se é uma função de , então também vai ter que ser! Dessa forma o semiperímetro vai ser também. Beleza, dá uma olhada então na altura : ela sempre parte do eixo e termina na curva ! Opa, então vai ser exatamente a curva!
Juntando à fórmula do semiperímetro:
E como:
O perímetro vai ser:
Passo 3
Agora que temos a função perímetro, borá otimizar ela! Pra otimizar, primeiro temos que achar os pontos críticos, não é? Então borá calcular a primeira derivada:
Igualando a primeira derivada à , vamos ter:
Mas agora, será que esse é mesmo um ponto de máximo? Pra isso vamos checar o sinal da derivada antes e depois do ponto crítico. Analisando antes, com , por exemplo, temos:
E analisando depois, temos, pra por exemplo:
Se antes a inclinação da reta tangente, expressa por , era positiva e depois negativa, então é sim um ponto de máximo! Como:
Pra gente achar as dimensões é só a gente aplicar o ponto crítico!
Mas como é só metade da base do retângulo, as dimensões do retângulo de maior perímetro vão ser: