Problemas de Otimização
Encontre o menor segmento de reta contido no primeiro quadrante ligando o eixo ao eixo e passando pelo ponto .
Passo 1
A ideia inicial é fazer um esboço geral da situação para uma reta qualquer que passe em e toque os dois eixos para poder determinar parâmetros que ajudem a determinar a função para ser otimizada.
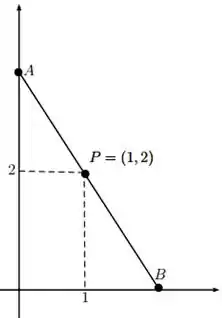
Chamando de o ponto onde a reta toca o eixo e o ponto onde toca o eixo podemos, por semelhança de triângulos, encontrar as relações seguintes entre as medidas de altura e de base dos triângulos da figura:
Além disso, podemos observar que o segmento será dado, por Pitágoras, pela raiz da soma dos quadrados da base e da altura do triângulo maior:
Das relações de semelhança, podemos tirar que . Com isso, a nossa função para otimizar será essa aqui:
Passo 2
Derivando esse cara e o igualando a :
Como , temos que ter para otimizar a função.
Agora repara o seguinte, para e para , o mínimo possível de acordo com o problema, temos . Com isso, fica visível que, se só achamos um ponto crítico, que será um mínimo. Enfim, o mínimo é o :
Efetuando as racionalizações, semelhante ao exemplo:
Obteremos...