Seja um ponto da parábola , com .
- Escreva uma função que represente a área do triângulo determinado pelos pontos , e .
- Encontre o valor de tal que a área do triangulo do item anterior seja máxima. Justifique sua resposta!
Passo 1
Vamos para a letra . Bem, se o ponto pertence a parábola , então . Dessa maneira, o triângulo será:
Como, pelo enunciado:
Então:
Sendo , o ponto de altura máxima do triângulo. Traçando-o no plano cartesiano:
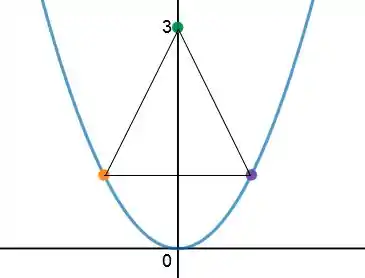
Assim, pela fórmula da área do triângulo:
Passo 2
Agora que temos a expressão da área, vamos encontrar o valor de que a maximiza. O máximo dá área pode ocorrer somente nos pontos críticos, quando a derivada é zero ou não existe. Vamos derivar então:
Portanto, os pontos críticos são:
Como , só nos interessa . Precisamos determinar se é um ponto de máximo. Vamos fazer isso usando o teste da segunda derivada, uma vez que é fácil de derivar:
Para , temos:
Como para , concluímos que esse é um ponto de máximo pelo teste da segunda derivada. Nesse ponto:
Enquanto, nos extremos:
Mostrando que esse é um ponto de máximo global.
Resposta
- .