Calcule o fluxo através de ( = normal unitária exterior), para:
e o elipsóide ;
Passo 1
Eaew, belezinha?
Precisamos calcular o fluxo do seguinte campo vetorial
através da superfície
O cálculo de fluxos pode ser feito através da seguinte expressão
Acima temos o teorema de Gauss, descobrir se é interessante expandir o lado esquerdo ou o lado direito da expressão acima é caminho! Bora lá!
Passo 2
Vamos calcular a divergência do campo vetorial, nós temos que
em que . Calculando as derivadas parciais temos então que
Ficou até bastante simples! Talvez seja conveniente expandir a nossa integral tripla! Bora lá!
Passo 3
Para expandir a integral tripla precisamos estabelecer os limites de integração convenientes para descrever o nosso elipsóide, o interessante será utilizar coordenadas esféricas nesta missão, temos que
Para enxergar melhor a mudança de variáveis, vamos fazer a seguinte identificação
, e
de forma que o nosso elipsóide toma o formato de uma esfera nessa escolha
Temos que tomar o cuidado de que se mudamos as variáveis, precisamos calcular o jacobiano através da definição
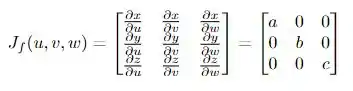
a matriz do lado direito já está calculada para a nossa mudança! Calculando o determinante, temos que o jacobiano se torna
e, desta forma, podemos escrever a nossa integral como
Mas ainda está chato decidir quais são os limites de integração! Para isso, vamos fazer uma segunda mudança de coordenadas!
Passo 4
Agora nós temos uma esfera, e portanto, podemos usar coordenadas esféricas da forma
, e
e, o jacobiano já conhecido como
de forma que a nossa integral se torna
Agora fica fácil! Temos uma esfera de raio , portanto, as coordenadas simplesmente variam em , e . O que nos falta é resolver a integral
Vamos começar com a integração em ! Vem comigo!
Passo 5
Integrando primeiro em , temos que
Para a integral que separei precisaremos usar a relação de meio ângulo para o seno, e escrever
Resolvendo usando as integrais que já conhecemos, temos que
Portanto, resta para resolvermos a seguinte integral
Vamos resolver agora a integral em !
Passo 6
Separando a integral em , temos que
para resolver essa integral será conveniente escrever a expressão acima como , e usar a identidade trigonométrica para reescrever o , vamos ficar com
A primeira dessas duas integrais já é conhecida, podemos escrever que
e, para a segunda integral precisamos usar a substituição simples
e
usando que e que , obtemos
avaliando os limites de integração temos que
a nossa integral se torna então
Voltando estes resultados em nossa integral original, temos que
Falta só mais uma integral! Bora lá!
Passo 7
A integral em pode ser resolvida usando a regra do polinômio para integrais, temos que
de forma que temos o nosso resultado final como
A questão foi isso! Te vejo na próxima! Tchau Tchau!