Seja o campo vetorial definido por
Considere e S a superfície que é a fronteira de com orientação positiva. Calcule
Passo 1
Vamos primeiro visualizar o que é .
Da primeira equação
Olhando para a segunda desigualdade e considerando:
e, separadamente, vamos ter respectivamente as equações:
Isso nos plano , e terá a mesma forma:
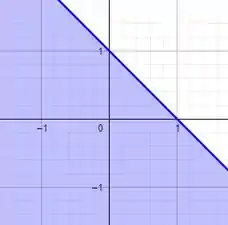
Juntando a figura com as outras desigualdade e teremos o sólido:
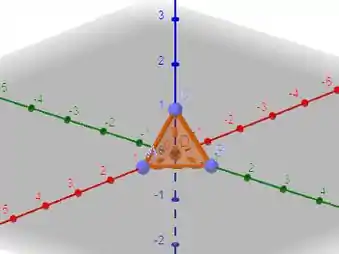
Passo 2
Como queremos a integral de superfície do sólido podemos utilizar o teorema de Gauss:
Temos que primeiro verificar se todas as condições são satisfeitas:
- A superfície deve ser fechada e assim definir um volume
- Não deve possuir singularidade
- A normal deve ser orientada para fora, no sentido contrário ao espaço definido pela superfície, sendo assim a orientação positiva.
No nosso caso todas as condições são satisfeitas.
Passo 3
Voltando para a equação do teorema de Gauss temos E é o espaço confinado pela superfície
Calculando o divergente do campo vetorial :
Onde:
Realizando a conta do divergente podemos ver que o resultado é 3. Assim:
Essa integral tripla da direita é nada mais nada menos que 3 vezes o volume do espaço .
Passo 4
Para fazer o cálculo da integral tripla, vamos considerar que a região é do tipo pois varia entre duas funções e .
Podemos escrever dessa forma:
A região é uma área que pode ser definida do tipo igual para integral dupla tendo variando entre constante e variando entre duas funções e
Podemos escrever a região dessa forma:
A integral tripla então vai ficar: