USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 17c
Seja , onde . Calcule , onde é a normal unitária exterior a nos seguintes casos:
é uma superfície fechada lisa por partes que contém a origem em seu interior.
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
em que o campo vetorial é dado por
onde . E, a nossa superfície obedece às seguintes condições
é uma superfície fechada lisa por partes que contém a origem em seu interior.
Parece complicado, mas essa é uma questão conceitual! O segredo está no fato de que o nosso campo vetorial tem uma simetria esférica partindo da origem e a superfície contém a origem! Vem comigo!
Passo 2
Vamos fazer um breve esquema aqui do que seria a nossa situação
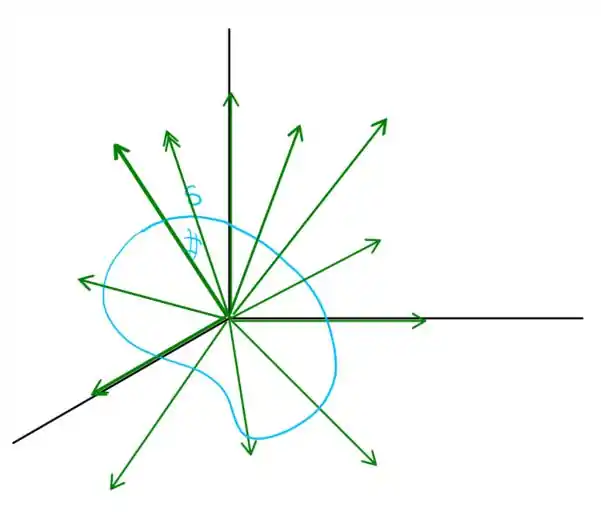
O fluxo do campo vetorial através de uma superfície está relacionado a quantidade que entra (ou sai) pela superfície. Se a superfície é fechada, e o campo vetorial é interno a sua superfície, necessariamente todas as setas estão saindo, portanto, temos que
Ainda mais, note que independentemente do formato da superfície, a quantidade de setinhas que atravessam é a mesma, portanto, para toda superfície o resultado será o mesmo (sob as condições do enunciado). Isso nos permite usar qualquer superfície para calcular o fluxo acima, nesta mesma questão fizemos para o caso da esfera! Que é uma superfície lisa fechada que contém a origem, e obtemos o resultado
Isso é um dos “poderes” do teorema de Gauss! E vai ser extremamente útil quando estiver calculando campos elétricos em Eletromagnetismo! A questão foi isso! Te vejo na próxima!