Use o teorema do divergente para calcular o fluxo de
Através da superfície do sólido limitado pelo cilindro e pelos planos e .
Passo 1
Vamos começar fazendo um gráfico dessa região. Como a variável que “falta” na equação do cilindro é , sabemos que esse é o seu eixo de simetria, ou seja, o cilindro está “deitado” dessa forma:
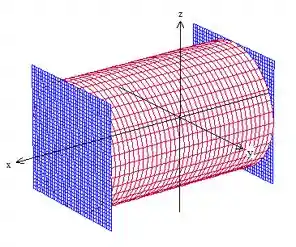
Como a região limitada por é fechada, sendo orientada positivamente, podemos aplicar o Teorema de Gauss:
Passo 2
Agora precisamos calcular . Temos:
Passo 3
Agora vamos montar a integral
Onde é o volume que vimos no passo 1.
Passo 4
Vamos agora, descrever essa região . Como nós temos um cilindro e nossa função a ser integrada , parece uma boa usar coordenadas cilíndricas. Mas não as coordenadas cilíndricas convencionais, que estamos acostumados a usar:
Já que o nosso cilindro está deitado, seu eixo de simetria não é o , mas o , vamos fazer essa substituição aqui:
É como se a gente tivesse trocado as coordenadas! Como o eixo de simetria é o , essa é a variável que não muda (), as outras duas, e , nós vamos chamar de e , como fazíamos antes. O Jacobiano é o mesmo, pois, afinal, é uma mudança cilíndrica.
Então, equação do cilindro se transforma em .
Como podemos ver pela figura, . Já que temos uma volta completa no plano , temos . Os valores de variam desde o eixo , onde até o cilindro, onde , portanto, .
Isso nos dá
Repare que os diferenciais são , não !
Passo 5
Agora vamos resolver a integral. Integrando em relação a :
Agora em relação a :
Finalmente, em relação a :