UNICAMP. Calculo 2. 2021.2 - 5ª Tarde. Prova: P3. Questão 4.
Use o Teorema do Divergente para calcular o fluxo do campo vetorial
através da superfície , (a metade superior da esfera de raio e centro na origem). Considere orientada com o vetor normal unitário que aponta para cima (isto é, a terceira coordenada do vetor normal é positiva). (Sugestão: Usar o Teorema da Divergência)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão foi pedido pra aplicarmos o teorema da divergência ou também podemos chamar de teorema de Gauss para calcular o fluxo do campo vetorial .
No caso é dado por
E a superfície que queremos analisar é dada pela equação sendo que e o vetor normal é orientado para cima.
Ok, mas como fazemos isso?? 🤔🤔
O Teorema de Gauss nos diz que podemos reescrever a integral de como
Já o divergente de é dado por
Entendeu? Bora começar! 😁
Passo 2
Vamos começar pelo divergente de
Se , então
Calculando as derivadas pelo método de derivação polinomial, temos
Com isso, obtemos
Substituindo na integral
Tranquilo até aqui? 👀
Passo 3
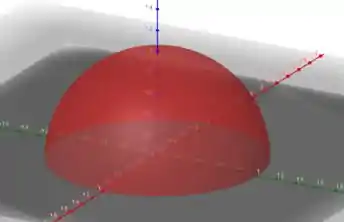
Vamos dar uma olhada na nossa superfície .
Ela é delimitada pela equação para , ou seja, uma semiesfera de raio .
Para coordenadas esféricas sabemos que onde é o raio.
Convertendo nossa integral para coordenadas esféricas onde
E os limites de integração?
Como nossa superfície é uma semiesfera, temos
Se olharmos para aquela colinha de referência de , e
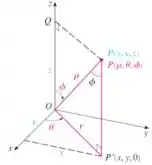
Vemos que está variando de a , está variando de a e está variando de a .
Com isso, nossa integral será
Agora só nos resta calcular essa integral.
Bora lá!
Passo 4
Integrando com relação a pelo método de integração polinomial
Aplicando os limites de integração
Com isso, temos
Integrando com relação a , sabemos que pelo teorema fundamental do cálculo, a integral de é igual a . Portanto
Aplicando os limites de integração
Por fim, integramos com relação a
Como é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.
Aplicando os limites de integração
Portanto, vemos que a integral do fluxo do campo vetorial através da superfície é .
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
