Use o Teorema do divergente para calcular
, onde e é a superfície do sólido limitado pelo paraboloide e pelo plno orientado positivamente.
Passo 1
O teorema do divergente (Gauss) nos diz que:
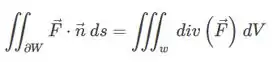
Onde
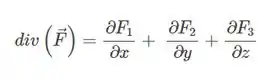
Passo 2
Vamos então observar nossa região:
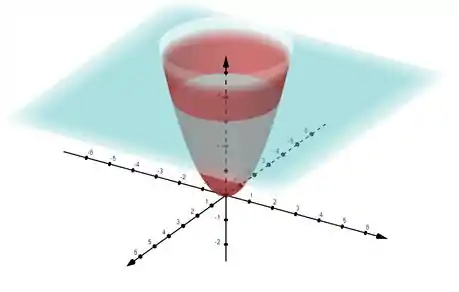
Escrevendo nossa região em coordenadas cilíndricas ficamos com:
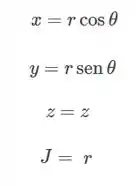
Assim ficamos com:
Igualando as duas funções que restrigem o intervalo:
E o dando uma volta completa, 0 a
Passo 3
Vamos escrever então o que a gente tem até agora, sem esquecer o Jacobiano:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,