A integral de superfície onde é , com e orientada com a normal exterior é
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
Temos que a notação com produto exterior pode ser escrita da seguinte forma:
.
Temos então que:
sendo,
e a superfície considerada é a semi-esfera
.
Como este campo vetorial é complicado vamos tentar utilizar o teorema da divergência de Gauss dado por
em que é a superfície fronteira ao sólido , não necessariamente a nossa superfície , mas elas estão relacionadas, vamos ver isso durante o exercício. Vamos lá!
Passo 2
A nossas região pode ser visualizada como
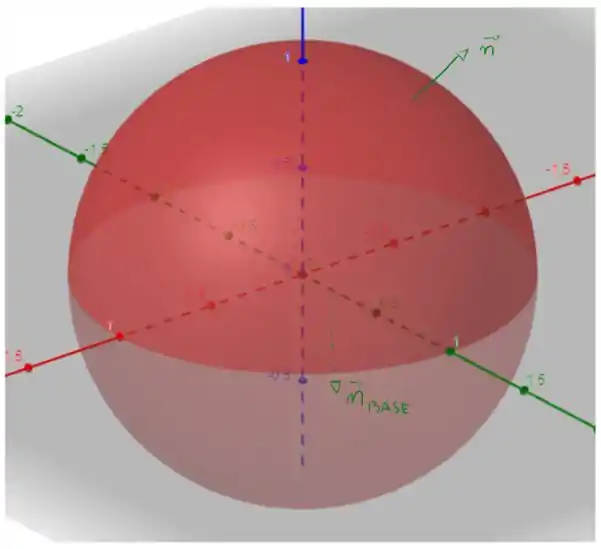
A nossa superfície é a cúpula de um sólido , que tem como base um plano. Então, podemos considerar o teorema da divergência de Gauss, usando um da forma
que é fronteira de , e portanto, a nossa integral pode ser identificada como
A integral que nós queremos é apenas uma parte do lado esquerdo do teorema de Gauss, portanto, vamos ter que calcular as outras duas componentes. No entanto, isso é um pouco mais fácil do que expandir a integral de superfície normalmente! Saca só!
Passo 3
Vamos começar calculando o lado direito, temos que a divergência do campo é tal que
em que . Substituindo então o campo dado no enunciado, temos que
fazendo as derivadas parciais (lembre-se que variáveis que não estão sendo derivadas são tomadas como constantes), temos que
de forma que
A integral é simplesmente o volume da meia esfera, como temos que uma esfera tem volume dado por
portanto, meia esfera tem o volume dado por
e, essa esfera tem . Portanto, podemos escrever que
Desta maneira tudo que precisamos fazer é resolver a integral de superfície restante! Bora lá!
Passo 4
O nosso problema está resumido em
Pela nossa figura, e levando em consideração que a normal considerada para a nossa superfície é tal que estamos considerando as normais externas, temos que a base tem um vetor normal dado por
Usando o formato de nosso campo vetorial, e resolvendo o produto escalar na integral de superfície, temos que
como temos que a base está em , a nossa superfície é obtida como a circunferência
de forma que podemos usar coordenadas polares da seguinte maneira
e
de forma que . Como temos uma circunferência de raio , a integração se torna simplesmente
Vamos resolver essa integral rapidamente! Saca só!
Passo 5
Resolvendo primeiro a integral em (a ordem não importa aqui pois os limites são todos constantes), temos que
Portanto, temos que
Sendo assim, o nosso problema se torna
ou simplesmente
Ou seja, alternativa . A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta